Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T22:54:30.683Z Has data issue: false hasContentIssue false
  • English
  • Français

Laplace Equations and the Weak Lefschetz Property

Published online by Cambridge University Press:  20 November 2018

Emilia Mezzettiaaa ,
Rosa M. Miré-Roig  and
Giorgio Ottaviani
Emilia Mezzettiaaa
Affiliation:
Dipartimento di Matematica e Geoscienze, Università di Trieste, Via Valerio 12/1, 34127 Trieste, Italy, e-mail: mezzette@units.it
Rosa M. Miré-Roig
Affiliation:
Facultat de Matemàtiques, Department d'Algebra i Geometria, Gran Via des les Corts Catalanes 585, 08007 Barcelona, Spain, e-mail: miro@ub.edu
Giorgio Ottaviani
Affiliation:
Dipartimento di Matematica, Università di Firenze, Viale Morgagni 67/A I-50134 Firenze, Italy, e-mail: ottavian@math.unifi.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that $r$ independent homogeneous polynomials of the same degree $d$ become dependent when restricted to any hyperplane if and only if their inverse system parameterizes a variety whose 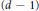$(d-1)$- osculating spaces have dimension smaller than expected. This gives an equivalence between an algebraic notion (called the Weak Lefschetz Property) and a differential geometric notion, concerning varieties that satisfy certain Laplace equations. In the toric case, some relevant examples are classified, and as a byproduct we provide counterexamples to Ilardi's conjecture.

Keywords

13E1014M2514N0514N1553A20osculating spaceweak Lefschetz propertyLaplace equationstoric threefold
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 3 , 01 June 2013 , pp. 634 - 654
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Brenner, H. and Kaid, A., Syzygy bundles on P2and the weak Lefschetz property. Illinois J. Math.51(2007), no. 4, 1299–1308.Google Scholar
[2] Cook, D. II andNagel, U., Enumerations deciding the weak Lefschetz property. arxiv:1105.6062v1. Google Scholar
[3] Dye, R. H., The extraordinary higher tangent spaces of certain quadric intersections. Proc. Edinburgh Math. Soc. (2) 35(1992), no. 3, 437–447. http://dx.doi.org/10.1017/S0013091500005721 Google Scholar
[4] Edge, W. L., A new look at the Kummer surface. Canad. J. Math. 19(1967), 952–967. http://dx.doi.org/10.4153/CJM-1967-087-5 Google Scholar
[5] Franco, D. and Ilardi, G., On a theorem of Togliatti. Int. Math. J. 2(2002), no. 4, 379–397.Google Scholar
[6] Fulton, W., Intersection theory. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 2, Springer-Verlag, Berlin 1984.Google Scholar
[7] Fulton, W. and Harris, J., Representation theory, a first course. Graduate Texts in Mathematics, 129, Springer-Verlag, New York, 1991.Google Scholar
[8] Gel’fand, I. M., Kapranov, M. M., and Zelevinsky, A. V., Discriminants, resultants and multidimensional determinants. Mathematics: Theory & Applications, Birkhäuser Boston, Boston, MA, 1994 Google Scholar
[9] Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/. Google Scholar
[10] Griffiths, P. and Harris, J., Algebraic geometry and local differential geometry. Ann. Sci. école Norm. Sup.(4) 12(1979), no. 3, 355–452.Google Scholar
[11] Ilardi, G., Togliatti systems. Osaka J. Math. 43(2006), no. 1, 1–12.Google Scholar
[12] Mezzetti, E. and Tommasi, O., On projective varieties of dimension n + k covered by k-spaces. Illinois J. Math. 46(2002), no. 2, 443–465.Google Scholar
[13] Migliore, J., Miré-Roig, R. M., and Nagel, U., Monomial ideals, almost complete intersections and the weak Lefschetz property. Trans. Amer. Math. Soc. 363(2011), no. 1, 229–257. http://dx.doi.org/10.1090/S0002-9947-2010-05127-X Google Scholar
[14] Okonek, C., Schneider, M., and Spindler, H., Vector bundles on complex projective spaces. Progress in Mathematics, 3, Birkhäuser, Boston, MA, 1980.Google Scholar
[15] Perkinson, D., Inflections of toric varieties. Michigan Math. J. 48(2000), 483–515. http://dx.doi.org/10.1307/mmj/1030132730 Google Scholar
[16] Segre, C., Su una classe di superfici degl’iperspazi legate colle equazioni lineari alle derivate parziali di 2 oordine. Atti R. Accad. Scienze Torino 42(1906-07), 559–591.Google Scholar
[17] Stanley, R. P., The number of faces of a simplicial convex polytope. Adv. in Math. 35(1980), no. 3, 236–238. http://dx.doi.org/10.1016/0001-8708(80)90050-X Google Scholar
[18] Stanley, R. P., Weyl groups, the hard Lefschetz theorem, and the Sperner property. SIAM J. Algebraic Discrete Methods 1(1980), no. 2, 168–184. http://dx.doi.org/10.1137/0601021 Google Scholar
[19] Togliatti, E., Alcuni esempi di superfici algebriche degli iperspazi che rappresentano un’equazione di Laplace. Comm Math. Helvetici 1(1929), 255–272.Google Scholar
[20] Togliatti, E., Alcune osservazioni sulle superfici razionali che rappresentano equazioni di Laplace. Ann. Mat. Pura Appl. (4) 25(1946), 325–339. http://dx.doi.org/10.1007/BF02418089 Google Scholar
[21] Vallès, J., Variétés de type Togliatti,C. R. Acad. Sci. Paris, Ser. I 343 (2006), 411–414 http://dx.doi.org/10.1016/j.crma.2006.08.004 Google Scholar
[22] J.Watanabe, , The Dilworth number of Artinian rings and finite posets with rank function. Commutative algebra and combinatorics (Kyoto, 1985), Advanced Studies in Pure Math., 11, North Holland, Amsterdam, 1987, pp. 303–312.Google Scholar