Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Erdélyi, Tamás
2011.
Sieve-Type Lower Bounds for the Mahler Measure of Polynomials on Subarcs.
Computational Methods and Function Theory,
Vol. 11,
Issue. 1,
p.
213.
Choi, Stephen
and
Mossinghoff, Michael J.
2011.
Average Mahler’s measure andLpnorms of unimodular polynomials.
Pacific Journal of Mathematics,
Vol. 252,
Issue. 1,
p.
31.
Choi, Stephen
and
Erdélyi, Tamás
2014.
Average Mahler’s measure and 𝐿_{𝑝} norms of Littlewood polynomials.
Proceedings of the American Mathematical Society, Series B,
Vol. 1,
Issue. 10,
p.
105.
Erdélyi, Tamás
2015.
Flatness of conjugate reciprocal unimodular polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 432,
Issue. 2,
p.
699.
Choi, Stephen
and
Erdélyi, Tamás
2015.
Sums of monomials with large Mahler measure.
Journal of Approximation Theory,
Vol. 197,
Issue. ,
p.
49.
Erdélyi, Tamás
2016.
The Mahler Measure of the Rudin–Shapiro Polynomials.
Constructive Approximation,
Vol. 43,
Issue. 3,
p.
357.
Bell, Jason
and
Shparlinski, Igor E.
2017.
Power series approximations to Fekete polynomials.
Journal of Approximation Theory,
Vol. 222,
Issue. ,
p.
132.
Erdélyi, Tamás
2018.
Improved Lower Bound for the Mahler Measure of the Fekete Polynomials.
Constructive Approximation,
Vol. 48,
Issue. 2,
p.
283.
Erdélyi, Tamás
2020.
The asymptotic value of the Mahler measure of the Rudin-Shapiro polynomials.
Journal d'Analyse Mathématique,
Vol. 142,
Issue. 2,
p.
521.
Erdélyi, Tamás
2020.
Trigonometric Sums and Their Applications.
p.
29.
Erdélyi, Tamás
2020.
ON THE OSCILLATION OF THE MODULUS OF THE RUDIN–SHAPIRO POLYNOMIALS ON THE UNIT CIRCLE.
Mathematika,
Vol. 66,
Issue. 1,
p.
144.
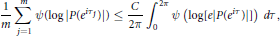 $$\frac{1}{m}\underset{j=1}{\overset{m}{\mathop{\sum }}}\,\,\psi \left( \log \,|P({{e}^{i\tau j}})| \right)\,\le \,\frac{C}{2\pi }\,\int_{0}^{2\pi }{\psi }\,\left( \log [e\,|P({{e}^{i\tau }})|] \right)\,d\tau ,$$
$$\frac{1}{m}\underset{j=1}{\overset{m}{\mathop{\sum }}}\,\,\psi \left( \log \,|P({{e}^{i\tau j}})| \right)\,\le \,\frac{C}{2\pi }\,\int_{0}^{2\pi }{\psi }\,\left( \log [e\,|P({{e}^{i\tau }})|] \right)\,d\tau ,$$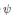 $\psi$ is convex and increasing,
$\psi$ is convex and increasing, 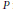 $P$ is a polynomial or an exponential of a potential, and the constant
$P$ is a polynomial or an exponential of a potential, and the constant 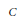 $C$ depends on the degree of
$C$ depends on the degree of 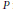 $P$, and the distribution of the points
$P$, and the distribution of the points 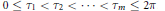 $0\,\le \,{{\tau }_{1}}\,<\,{{\tau }_{2}}\,<\,\cdots \,<\,{{\tau }_{m}}\,\le \,2\pi$. The method allows greater generality and is in some ways simpler than earlier ones. We apply our results to estimate the Mahler measure of Fekete polynomials.
$0\,\le \,{{\tau }_{1}}\,<\,{{\tau }_{2}}\,<\,\cdots \,<\,{{\tau }_{m}}\,\le \,2\pi$. The method allows greater generality and is in some ways simpler than earlier ones. We apply our results to estimate the Mahler measure of Fekete polynomials.