Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T10:04:59.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice Octahedra

Published online by Cambridge University Press:  20 November 2018

L. J. Mordell
L. J. Mordell*
Affiliation:
Mount Allison University Sackville, New Brunswick, Canada St. Johns College, Cambridge, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ai, A2, … , An be n linearly independent points in n-dimensional Euclidean space of a lattice Λ. The points ± A1, ±A2, . . , ±An define a closed n-dimensional octahedron (or “cross poly tope“) K with centre at the origin O. Our problem is to find a basis for the lattices Λ which have no points in K except ±A1, ±A2, … , ±An.

Let the position of a point P in space be defined vectorially by

1

where the p are real numbers. We have the following results.

When n = 2, it is well known that a basis is

2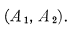

When n = 3, Minkowski (1) proved that there are two types of lattices, with respective bases

3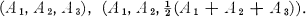

When n = 4, there are six essentially different bases typified by A1, A2, A3 and one of

4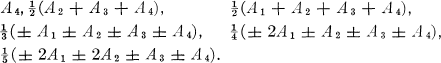

In all expressions of this kind, the signs are independent of each other and of any other signs. This result is a restatement of a result by Brunngraber (2) and a proof is given by Wolff (3).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 297 - 302
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Minkowski, H., Gesammelte Abhandlungen, Bd. II.Google Scholar
2. Brunngraber, E., Ueber Punktgitter (Dissertation, Wien, 1944).Google Scholar
3. Wolff, K.M., Monatsh. Math., 58 (1954), 38–56.Google Scholar
4. Blichfeldt, H.F., Monatsh. Math., 42-48 (1935-6), 410–414.Google Scholar