Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-15T17:27:27.913Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone and E-Schauder Bases of Subspaces

Published online by Cambridge University Press:  20 November 2018

John P. Russo
John P. Russo*
Affiliation:
Andrews University, Berrien Springs, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The notions of monotone bases and bases of subspaces are well known in a normed linear space setting and have obvious extensions to pseudo-metrizable linear topological spaces. In this paper, these notions are extended to arbitrary linear topological spaces. The principal result gives a list of properties that are equivalent to a sequence (Mi) of complete subspaces being an e-Schauder basis of subspaces for the closed linear span of 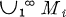. A corollary of this theorem is the fact that an e-Schauder basis for a dense subspace of a linear topological space is an e-Schauder basis for the whole space.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 233 - 241
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

Some of the results of this paper appear in a dissertation submitted to the Florida State University in partial fulfilment of the degree of Doctor of Philosophy.

This research was supported in part by National Science Foundation Grant GP-2179.

References

1. Grinbluym, M. M., On the representation of a space of type B in the form of a direct sum of subspaces, Dokl. Akad. Nauk SSSR (N.S.), 70 (1950), 749–752.Google Scholar
2. Kelley, J. L., Namioka, I., et al., Linear topological spaces (Princeton, 1963).10.1007/978-3-662-41914-4CrossRefGoogle Scholar
3. McArthur, C. W. and Retherford, J. R., Uniform and equicontinuous Schauder bases of subspaces, Can. J. Math., 17 (1965), 207–212.Google Scholar
4. Retherford, J. R. and McArthur, C. W., Some remarks on bases in linear topological spaces, Math. Ann., 164 (1966), 38–41.Google Scholar
5. Wilansky, A., Functional analysis (New York, 1964).Google Scholar