Published online by Cambridge University Press: 20 November 2018
Let G be a locally compact second countable group, let X be a locally compact second countable Hausdorff space, and view C(X, T) as a trivial G-module. For G countable discrete abelian, we construct an isomorphism between the Moore cohomology group Hn(G, C(X, T)) and the direct sum Ext(Hn-1(G), Ȟl(βX, Ζ)) ⊕ C(X, Hn(G, T)); here Ȟ1 (βX, Ζ) denotes the first Čech cohomology group of the Stone-Čech compactification of X, βX, with integer coefficients. For more general locally compact second countable groups G, we discuss the relationship between the Moore group H2(G, C(X, T)), the set of exterior equivalence classes of element-wise inner actions of G on the stable continuous trace C*-algebra C0(X) ⊗ 𝒦, and the equivariant Brauer group BrG(X) of Crocker, Kumjian, Raeburn, and Williams. For countable discrete abelian G acting trivially on X, we construct an isomorphism 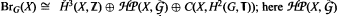 is the group of equivalence classes of principal Ĝ bundles over X first considered by Raeburn and Williams.
is the group of equivalence classes of principal Ĝ bundles over X first considered by Raeburn and Williams.