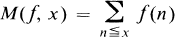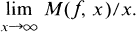Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hildebrand, Adolf
1988.
An Erdős-Wintner theorem for differences of additive functions.
Transactions of the American Mathematical Society,
Vol. 310,
Issue. 1,
p.
257.
Hildebrand, Adolf
1989.
Number Theory.
Vol. 1383,
Issue. ,
p.
76.
Elliott, P.D.T.A.
1989.
The value distribution of differences of additive arithmetic functions.
Journal of Number Theory,
Vol. 32,
Issue. 3,
p.
339.
Elliott, P. D. T. A.
1990.
Séminaire de Théorie des Nombres, Paris 1987–88.
Vol. 81,
Issue. ,
p.
63.
ELLIOTT, P. D. T. A.
1990.
Séminaire de Théorie des Nombres, Paris 1987–88.
Vol. 22,
Issue. ,
p.
63.
Indlekofer, K. -H.
and
Manstavičius, E.
1993.
Functional limit theorems for additive arithmetic functions on intervals.
Lithuanian Mathematical Journal,
Vol. 33,
Issue. 3,
p.
217.
Croot, Ernest S.
2003.
On the oscillations of multiplicative functions taking values ±1.
Journal of Number Theory,
Vol. 98,
Issue. 1,
p.
184.
Elliott, P. D. T. A.
2008.
Monotone additive functions on shifted primes.
The Ramanujan Journal,
Vol. 15,
Issue. 1,
p.
87.
Elliott, P. D. T. A.
2017.
Analytic Number Theory, Modular Forms and q-Hypergeometric Series.
Vol. 221,
Issue. ,
p.
267.