Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T20:06:57.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Nori Motives of Curves With Modulus and Laumon 1-motives

Published online by Cambridge University Press:  20 November 2018

Florian Ivorra  and
Takao Yamazaki
Florian Ivorra
Affiliation:
Institut de recherche mathématique de Rennes, UMR 6625 du CNRS, Université de Rennes 1, Campus de Beaulieu, 35042 Rennes cedex (France) email: florian.ivorra@univ-rennes1.fr
Takao Yamazaki
Affiliation:
Institute of mathematics, Tohoku University, Aoba, Sendaï, 980-8578 (Japan) email: ytakao@math.tohoku.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 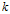$k$ be a number field. We describe the category of Laumon 1-isomotives over 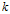$k$ as the universal category in the sense of M. Nori associated with a quiver representation built out of smooth proper 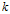$k$-curves with two disjoint effective divisors and a notion of 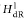$H_{\text{dR}}^{1}$ for such “curves with modulus”. This result extends and relies on a theorem of J. Ayoub and L. Barbieri-Viale that describes Deligne's category of 1-isomotives in terms of Nori's Abelian category of motives.

Keywords

19E1516G2014F42motivecurve with modulusquiver representation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 4 , 01 August 2018 , pp. 868 - 897
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Ayoub, Joseph and Barbieri-Viale, Luca, Nori 1-motives. Math. Ann. 361(2015), no. 1-2, 367–402. http://dx.doi.Org/10.1007/s00208-014-1069-8 Google Scholar
[2] Barbieri-Viale, Luca, On the theory of 1-motives. In: Algebraic cycles and motives, vol. 1, London Math. Soc. Lecture Note Ser., 343, Cambridge Univ. Press, Cambridge, 2007, pp. 55–101.Google Scholar
[3] Barbieri-Viale, L., Rosenschon, A., and Saito, M., Deligne's conjecture on 1-motives. Ann. of Math. (2) 158(2003), no. 2, 593–633. http://dx.doi.org/10.4007/annals.2003.158.593 Google Scholar
[4] Barbieri-Viale, Luca and Bertapelle, Alessandra, Sharp de Rham realization. Adv. Math. 222(2009), no. 4, 1308–1338. http://dx.doi.Org/10.1016/j.aim.2009.06.003 Google Scholar
[5] Barbieri-Viale, Luca and Srinivas, Vasudevan, Albanese and Picard 1-motives. Mem. Soc. Math. Fr. (N.S.) (2001), no. 87.Google Scholar
[6] Barbieri-Viale, Luca and Prest, Mike, Definable categories and T-motives. arxiv:1604.00153Google Scholar
[7] Barbieri-Viale, Luca, Caramello, Olivia, and Lafforgue, Laurent, Syntactic categories for Nori motives. arxiv:1 506.0611 3Google Scholar
[8] Deligne, Pierre, Théorie de Hodge. III, Inst. Hautes Études Sci. Publ. Math. (1974), no. 44, 5–77.Google Scholar
[9] Fakhruddin, Najmuddin, Notes of Nori's Lectures on Mixed Motives. TIFR, Mumbai, 2000.Google Scholar
[10] Gabriel, Pierre, Des catégories abéliennes. Bull. Soc. Math. France 90(1962), 323–448. http://dx.doi.Org/10.24033/bsmf.1583 Google Scholar
[11] Huber, Annette and Müller-Stach, Stefan, Periods and Nori motives. Ergebnisse der Mathematik und ihrer Grenzgebiete, 65. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer 2017.Google Scholar
[12] Ivorra, Florian, Perverse Nori motives. Math. Res. Lett. 24(2017), no. 4, 1097–1131. http://dx.doi.org/10.4310/MRL.2017.v24.n4.a8 Google Scholar
[13] Kato, Kazuya and Russell, Henrik, Albanese varieties with modulus and Hodge theory. Ann. Inst. Fourier (Grenoble) 62(2012), no. 2, 783–806. http://dx.doi.org/10.5802/aif.2694 Google Scholar
[14] Laumon, Gérard, Transformation de Fourier généralisée. arxiv:alg-geom/9603004v1Google Scholar
[15] Lekaus, Silke, On Albanese and Picard 1-motives with 𝔾a-factors. Manuscripta Math. 130(2009), no. 4, 495–522. http://dx.doi.org/10.1007/s00229-009-0299-7 Google Scholar
[16] Levine, Marc, Mixed motives. In: Handbook of K-theory. Springer, Berlin, 2005, pp. 429–521. http://dx.doi.org/10.1007/3-540-27855-9_10 Google Scholar
[17] Orgogozo, Fabrice, Isomotifs de dimension inférieure ou égale à un. Manuscripta Math. 115(2004), no. 3, 339–360. http://dx.doi.org/10.1007/s00229-004-0495-4 Google Scholar
[18] Rosenlicht, Maxwell, A universal mapping property of generalized jacobian varieties. Ann. of Math. (2) 66(1957), 80–88. http://dx.doi.Org/10.2307/1970118 Google Scholar
[19] Russell, Henrik, Generalized Albanese and its dual. J. Math. Kyoto Univ. 48(2008), no. 4, 907–949. http://dx.doi.org/10.1215/kjm/1250271323 Google Scholar
[20] Russell, Henrik, Albanese varieties with modulus over a perfect field. Algebra Number Theory 7(2013), no. 4, 853–892. http://dx.doi.Org/10.2140/ant.2013.7.853 Google Scholar
[21] Serre, Jean-Pierre, Groupes algébriques et corps de classes. Second ed. Publications de l'Institut Mathématique de l'Université de Nancago, 7. Actualites Scientifiques et Industrielles, 1264, Hermann, Paris, 1984.Google Scholar
[22] Serre, Jean-Pierre, Local fields. Graduate Texts in Mathematics, 67. Springer-Verlag, New York, 1979.Google Scholar
[23] Takeuchi, Mitsuhiro, Morita theorems for categories of comodules. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24(1977), no. 3, 629–644.Google Scholar