Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T06:14:15.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Norms of Complex Harmonic Projection Operators

Published online by Cambridge University Press:  20 November 2018

Valentina Casarino
Valentina Casarino*
Affiliation:
Dipartimento di Matematica, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Torino, Italia e-mail: casarino@calvino.polito.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we estimate the $\left( {{L}^{p}}-{{L}^{2}} \right)$-norm of the complex harmonic projectors 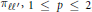$\pi \ell {\ell }',\,1\le p\le 2$, uniformly with respect to the indexes 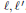$\ell,{\ell}'$. We provide sharp estimates both for the projectors 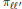${{\pi }_{\ell{\ell}'}}$, when 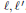$\ell,{\ell}'$ belong to a proper angular sector in 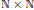$\mathbb{N}\,\times \,\mathbb{N}$, and for the projectors 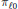${{\pi }_{\ell0}}$ and 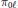${{\pi }_{0\ell}}$. The proof is based on an extension of a complex interpolation argument by C. Sogge. In the appendix, we prove in a direct way the uniform boundedness of a particular zonal kernel in the 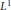${{L}^{1}}$ norm on the unit sphere of 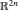${{\mathbb{R}}^{2n}}$.

Keywords

43A8533C5542B15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 6 , 01 December 2003 , pp. 1134 - 1154
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bonami, A. and Clerc, J. L., Sommes de Cesàro et moltiplicateurs des developpements en harmonic sphériques. Trans. Amer. Math. Soc. 183(1973), 223–263.Google Scholar
[2] Gelfand, I. M. and Shilov, G. E., Generalized Functions. Academic Press, N. Y., 1964.Google Scholar
[3] Giacalone, E., Stime uniformi per proiettori armonici su gruppi di Lie compatti di rang. 2. Boll. Un. Mat. Ital. B (7) 6(1992), 205–216.Google Scholar
[4] Giacalone, E. and Ricci, F., Norms of harmonic projection operators on compact Lie groups. Math. Ann. 280(1988), 21–31.Google Scholar
[5] Klimyk, A. U. and Vilenkin, N. Ja., Representation of Lie Groups and Special Functions. Kluwer Academic Publishers, 1993.Google Scholar
[6] Pólya, G. and Szegö, G., Problems and Theorems in Analysis, Vol. II. Springer Verlag, Fourth Ed., 1971.Google Scholar
[7] Sogge, C., Oscillatory integrals and spherical harmonics. Duke Math. J. 53(1986), 43–65.Google Scholar
[8] Stein, E. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces. Princeton University Press, Princeton, N.J., 1971.Google Scholar
[9] Szegö, G., Orthogonal Polynomials. Amer. Math. Soc. Colloq. Publ. 23, Amer. Math. Soc., 4th ed., Providence, R.I., 1974.Google Scholar
[10] Taylor, M., Pseudodifferential Operators. Princeton University Press, Princeton, N.J., 1981.Google Scholar