Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Petersen, G.M.
1967.
On the Structure of Well Distributed Sequences (IV) *)*)This work has been supported, in part, by the Air Force Office of Scientific Research, (Office of Aerospace Research), U.S. Air Force, under contract no AF 49 (638)–1401..
Indagationes Mathematicae (Proceedings),
Vol. 70,
Issue. ,
p.
128.
Zame, Alan
1967.
On the measure of well-distributed sequences.
Proceedings of the American Mathematical Society,
Vol. 18,
Issue. 4,
p.
575.


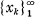 is said to be well distributed (mod 1) (3, 4, 5) if the limit
is said to be well distributed (mod 1) (3, 4, 5) if the limit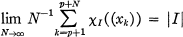
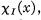 where (x) is the fractional part of
where (x) is the fractional part of 