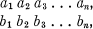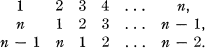Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Whitehead, Earl Glen
1979.
Four-discordant permutations.
Journal of the Australian Mathematical Society,
Vol. 28,
Issue. 3,
p.
369.
Hamilton, John R.
and
Mullen, Gary L.
1980.
How Many i-j Reduced Latin Rectangles are There?.
The American Mathematical Monthly,
Vol. 87,
Issue. 5,
p.
392.
Pranesachar, C. R.
1981.
Combinatorics and Graph Theory.
Vol. 885,
Issue. ,
p.
380.
Beker, Henry
and
Mitchell, Chris
1987.
Permutations with Restricted Displacement.
SIAM Journal on Algebraic Discrete Methods,
Vol. 8,
Issue. 3,
p.
338.
Godsil, C.D
and
McKay, B.D
1990.
Asymptotic enumeration of Latin rectangles.
Journal of Combinatorial Theory, Series B,
Vol. 48,
Issue. 1,
p.
19.
Shevelev, V. S.
1992.
Some problems of the theory of enumerating the permutations with restricted positions.
Journal of Soviet Mathematics,
Vol. 61,
Issue. 4,
p.
2272.
2015.
Latin Squares and their Applications.
p.
361.