No CrossRef data available.
Article contents
On 3-Manifolds with Sufficiently Large Decompositions
Published online by Cambridge University Press: 20 November 2018
Extract
In [6] it is shown that two (compact) orientable 3-manifolds which are irreducible, boundary irreducible and sufficiently large are homeomorphic if and only if there exists an isomorphism between the fundamental groups which respects the peripheral structure. In this note we extend this theorem to reducible 3-manifolds.
Any compact 3-manifold M has a decomposition into prime manifolds [1; 4].
1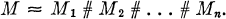
Here the connected sum of two bounded manifolds N1, N2 is denned by removing 3-balls B1 B2 in int N1, int N2, respectively, and glueing the resulting boundary spheres together. The M1's which occur in the decomposition (1) are either irreducible or handles (i.e., a fibre bundle over S1 with fibre S2). If (1) contains a fake 3-sphere, we assume it to be Mn.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1971
References
A correction has been issued for this article:
Linked content
Please note a has been issued for this article.


