Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T09:29:05.175Z Has data issue: false hasContentIssue false
  • English
  • Français

On Compact Perturbations of Operators

Published online by Cambridge University Press:  20 November 2018

Joel Anderson
Joel Anderson*
Affiliation:
California Institute of Technology, Pasadena, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently R. G. Douglas showed [4] that if V is a nonunitary isometry and U is a unitary operator (both acting on a complex, separable, infinite dimensional Hilbert space 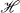), then V — K is unitarily equivalent to V ⊕ U (acting on 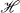⊕ 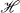) where K is a compact operator of arbitrarily small norm. In this note we shall prove a much more general theorem which seems to indicate "why" Douglas' theorem holds (and which yields Douglas' theorem as a corollary).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 1 , February 1974 , pp. 247 - 250
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Anderson, J. H., Commutators and the essential numerical range (to appear).Google Scholar
2. Berg, I. D., An extension of the Weyl-von Neumann theorem, Trans. Amer. Math. Soc. 160 (1971), 365–371.Google Scholar
3. Brown, A. and Halmos, P. R., Algebraic properties of Toeplitz operators, J. Reine Angew. Math. 213 (1964), 89–102.Google Scholar
4. Douglas, R. G., Banach algebra techniques in the theory of Toeplitz operators, Notes for lectures given at CMBS Regional Conference at the University of Georgia, June, 1972.Google Scholar
5. Fillmore, P. A., Stampfli, J. G., and Williams, J. P., On the essential numerical range, the essential spectrum, and a problem of Halmos (to appear in Acta. Sci. Math. (Szeged)).Google Scholar
6. Hartman, P. and Wintner, A., On the spectra of Toeplitz s matrices, Amer. J. Math. 72 (1950), 359–366.Google Scholar
7. Pearcy, C. and Salinas, N., Compact perturbations of seminormal operators, Indiana Univ. Math. J. (to appear).Google Scholar
8. Putnam, C. R., Eigenvalues and boundary spectra, Illinois J. Math. 12 (1968), 278–282.Google Scholar
9. Stampfli, J. G., Extreme points of the numerical range of a hyponormal operator, Michigan Math. J. 18 (1966), 87–89.Google Scholar
10. Stampfli, J. G. and Williams, J. P., Growth conditions and the numerical range in a Banach algebra, Tôhoku Math. J. 20 (1968), 417–424.Google Scholar