Article contents
On Self-Adjoint Factorization of Operators
Published online by Cambridge University Press: 20 November 2018
Extract
The main result of this paper is that every normal operator on an infinitedimensional (complex) Hilbert space ℋ is the product of four self-adjoint operators; our Theorem 4 is an actually stronger result. A large class of normal operators will be given which cannot be expressed as the product of three self-adjoint operators.
This work was motivated by a well-known resul t of Halmos and Kakutani (3) that every unitary operator on ℋ is the product of four symmetries, i.e., operators that are self-adjoint and unitary.
1. By “operator” we shall mean bounded linear operator. The space ℋ will be infinite-dimensional (separable or non-separable) unless otherwise specified. We shall denote the class of self-adjoint operators on ℋ by 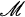 and that of symmetries by
and that of symmetries by  .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
References
- 4
- Cited by

