Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-16T01:02:23.372Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Continuity and Self-Injectivity of a Complete Regular Ring

Published online by Cambridge University Press:  20 November 2018

Yuzo Utumi
Yuzo Utumi*
Affiliation:
The State University of New York, Buffalo, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be a ring, and let (ei) be an orthogonal system of a finite number of idempotents. Then e = Σei has the following properties:

(i) Se Σ Sei and eS = Σ ei S.

(ii) The mappings v: Se → Π Sei and w: eS → Π ei S defined by v(x) = [xei] and w(x) = [ei x] respectively are isomorphisms.

Next assume that (ei)i∈I is a set of idempotents indexed by a totally ordered set I such that ei ej = 0 for every i < j. If I is finite, it is evident that

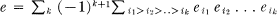
has the above two properties.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 404 - 412
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Amemiya, I. and Halperin, I., Complemented modular lattices, Can. J. Math., 11 (1959), 481–520.Google Scholar
2. Faith, Carl and Utumi, Yuzo, Intrinsic extensions of rings, Pacific J. Math., 14 (1964), 505–512.Google Scholar
3. Utumi, Yuzo, On continuous regular rings, Can. Math. Bull., 4 (1961), 63–69.Google Scholar
4. Utumi, Yuzo, On rings of which any one-sided quotient rings are two-sided, Proc. Amer. Math. Soc., 14 (1963), 141–147.Google Scholar