Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T08:47:21.414Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hausdorff and Trigonometric Moment Problems

Published online by Cambridge University Press:  20 November 2018

P. G. Rooney
P. G. Rooney*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a subset of BV(0, 1)—the space of functions of bounded variation on the closed interval [0, 1]. By the Hausdorff moment problem for K we shall mean the determination of necessary and sufficient conditions that corresponding to a given sequence μ = {μn|n = 0, 1, 2, …} there should be a function α ∈ K so that

(1)

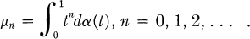
For various collections K this problem has been solved—see (3, Chapter III)

By the trigonometric moment problem for K we shall mean the determination of necessary and sufficient conditions that corresponding to a sequence c = {cn|n = 0, ± 1, ± 2, …} there should be a function α ∈ K so that

(2)

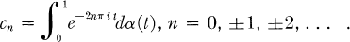
For various collections K this problem has also been solved—see, for example (4, Chapter IV, § 4). It is noteworthy that these two problems have been solved for essentially the same collections K.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 454 - 461
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Bochner, S., Vorlesungen über Fouriersche Intégrale (Leipzig, 1932).Google Scholar
2. Rooney, P. G., On the representation of sequences as Fourier coefficients, Proc. Amer. Math. Soc, 11 (1960), 762–768.Google Scholar
3. Widder, D. V., The Laplace transform (Princeton, 1941).Google Scholar
4. Zygmund, A., Trigonometric series I (Cambridge, 1959).Google Scholar