Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T05:49:39.020Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Local Lifting Properties of Operator Spaces

Published online by Cambridge University Press:  20 November 2018

Z. Dong
Z. Dong*
Affiliation:
Department of Mathematics, Zhejiang University, Hangzhou 310027, P.R.China and Department of Mathematics, University of Illinois-U.C., Urbana, Illinois 61801 email: dongzhe@zju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we mainly study operator spaces which have the locally lifting property 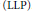$\left( \text{LLP} \right)$. The dual of any ternary ring of operators is shown to satisfy the strongly local reflexivity, and this is used to prove that strongly local reflexivity holds also for operator spaces which have the 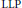$\text{LLP}$. Several homological characterizations of the 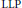$\text{LLP}$ and weak expectation property are given. We also prove that for any operator space 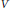$V$, 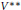${{V}^{**}}$ has the 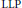$\text{LLP}$ if and only if 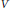$V$ has the 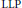$\text{LLP}$ and 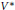${{V}^{*}}$ is exact.

Keywords

46L07operator spacelocally lifting propertystrongly locally reflexive
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1262 - 1278
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Blecher, D., Tensor products of operator spaces. II. Canad. J. Math. 44(1992), no. 1, 75–90.Google Scholar
[2] Blecher, D., The standard dual of an operator space. Pacific J. Math. 153(1992), no. 1, 15–30.Google Scholar
[3] Blecher, D. and Paulsen, V., Tensor products of operator spaces. J. Funct. Anal. 99(1991), no. 2, 262–292.Google Scholar
[4] Effros, E. G. and Haagerup, U., Lifting problems and local reflexivity for C* -algebras. Duke Math. J. 52(1985), no. 1, 103–128.Google Scholar
[5] Effros, E. G. and Ruan, Z.-J., On approximation properties for operator spaces. Internat. J. Math. 1(1990), no. 2, 163–187.Google Scholar
[6] Effros, E. G. and Ruan, Z.-J., Mapping spaces and lifting for operator spaces. Proc. London Math. Soc. 69(1994), no. 1, 171–197.Google Scholar
[7] Effros, E. G. and Ruan, Z.-J., The Grothendieck-Pietsch and Dvoretzky-Rogers theorem for operator spaces. J. Funct. Anal. 122(1994), no. 2, 428–450.Google Scholar
[8] Effros, E. G. and Ruan, Z.-J., On the analogues of integral mappings and local reflexivity for operator spaces. Indiana Univ. Math. J. 46(1997), no. 4, 1289–1310.Google Scholar
[9] Effros, E. G. and Ruan, Z.-J., Operator Spaces. London Mathematical Society Monographs 23, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[10] Effros, E. G., Junge, M. and Ruan, Z.-J., Integral mapping and the principle of local reflexivity for non-commutative L1 spaces. Ann. of Math. 151(2000), no. 1, 59–92.Google Scholar
[11] Effros, E. G., Ozawa, N. and Ruan, Z.-J., On injectivity and nuclearity for operator spaces. Duke Math. J. 110(2001), no. 3, 489–521.Google Scholar
[12] Harris, L., A generalization of C* -algebras. Proc. London Math. Soc. 42(1981), 331–361.Google Scholar
[13] Hestenes, M., A ternary algebra with applications to matrices and linear transformation. Arch. Rational Mech. Anal. 11(1962), 1315–1357.Google Scholar
[14] Junge, M., Factorization Theory for Spaces of Operators. Habilitationsschrift, Universität Kiel, 1996.Google Scholar
[15] Kaur, M. and Ruan, Z.-J., Local properties of ternary rings of operators and their linking C* -algebras. J. Funct. Anal. 195(2002), no. 2, 262–305.Google Scholar
[16] Kirchberg, E., On nonsemisplit extensions, tensor products and exactness of group C -algebras. Invent. Math. 112(1993), no. 3, 449–489.Google Scholar
[17] Kye, S. H. and Ruan, Z.-J., On the local lifting property for operator spaces. J. Funct. Anal. 168(1999), no. 2, 355–379.Google Scholar
[18] Pisier, G., Exact operator spaces. Recent advances in operator algebras. Astérisque No. 232(1995), 159–186.Google Scholar
[19] Pisier, G., Introduction to Operator Space Theory. London Mathematical Society Lecture Notes Series 294. Cambridge University Press, Cambridge, 2003.Google Scholar
[20] Ruan, Z.-J., Subspaces of C* -algebras. J. Funct. Anal. 76(1988), no. 1, 217–230.Google Scholar
[21] Ruan, Z.-J., Injectivity of operator spaces. Trans. Amer. Math. Soc. 315(1989), no. 1, 89–104.Google Scholar
[22] Zettl, H., A characterization of ternary rings of operators, Adv. in Math. 48 (1983), no. 2, 117–143.Google Scholar