Published online by Cambridge University Press: 20 November 2018
We extend the classical notion of an outer action  $\alpha $ of a group
$\alpha $ of a group 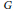 $G$ on a unital ring
$G$ on a unital ring 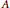 $A$ to the case when
$A$ to the case when  $\alpha $ is a partial action on ideals, all of which have local units. We show that if
$\alpha $ is a partial action on ideals, all of which have local units. We show that if  $\alpha $ is an outer partial action of an abelian group
$\alpha $ is an outer partial action of an abelian group 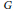 $G$, then its associated partial skew group ring
$G$, then its associated partial skew group ring 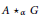 $A\,{{\star }_{\alpha }}\,G$ is simple if and only if
$A\,{{\star }_{\alpha }}\,G$ is simple if and only if 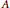 $A$ is
$A$ is 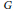 $G$-simple. This result is applied to partial skew group rings associated with two different types of partial dynamical systems.
$G$-simple. This result is applied to partial skew group rings associated with two different types of partial dynamical systems.