Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T21:26:14.095Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial Characters and Signed Quotient Hypergroups

Published online by Cambridge University Press:  20 November 2018

Margit Rösler  and
Michael Voit
Margit Rösler
Affiliation:
Zentrum Mathematik, Technische Universität München, Arcisstr. 21, D-80290 München, Germany email: roesler@ma.tum.de
Michael Voit
Affiliation:
Mathematisches Institut, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany email: voit@uni-tuebingen.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If $G$ is a closed subgroup of a commutative hypergroup $K$, then the coset space 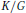$K/G$ carries a quotient hypergroup structure. In this paper, we study related convolution structures on 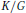$K/G$ coming fromdeformations of the quotient hypergroup structure by certain functions on $K$ which we call partial characters with respect to $G$. They are usually not probability-preserving, but lead to so-called signed hypergroups on 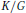$K/G$. A first example is provided by the Laguerre convolution on 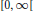$[0,\infty [$, which is interpreted as a signed quotient hypergroup convolution derived from the Heisenberg group. Moreover, signed hypergroups associated with the Gelfand pair 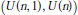$\left( U\left( n,1 \right),\,U\left( n \right) \right)$ are discussed.

Keywords

43A6233C2543A2043A90quotient hypergroupssigned hypergroupsLaguerre convolutionJacobi functions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 1 , 01 February 1999 , pp. 96 - 116
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Benson, C., Jenkins, J. and Ratcliff, G., Bounded K-spherical functions on Heisenberg groups. J. Funct. Anal. 105 (1992), 409–443.Google Scholar
[2] Berezansky, Yu. M. and Kaluzhny, A. A., Hypercomplex systems with locally compact bases. Selecta Math. Soviet. (2) 4 (1985), 151–200.Google Scholar
[3] Bloom, W. and Heyer, H., Harmonic Analysis of Probability Measures on Hypergroups. De Gruyter, Berlin-New York, 1995.Google Scholar
[4] Dunkl, C. F., The measure algebra of a locally compact hypergroup. Trans. Amer. Math. Soc. 179 (1973), 331– 348.Google Scholar
[5] Faraut, J., Analyse harmonique sur les pairs de Gelfand et les espaces hyperboliques. In: Analyse harmonique (Eds. Clerc, J.-L., Eymard, P., Faraut, J., Rais, M. and Takahashi, R.), Ch. IV, C. I. M. P. A., Nice, 1982.Google Scholar
[6] Flensted-Jensen, M., Spherical functions on a simply connected semisimple Lie group II. The Paley-Wiener theorem for the rank one case. Math. Ann. 228 (1972), 65–92.Google Scholar
[7] Flensted-Jensen, M. and Koornwinder, T. H., The convolution structure for Jacobi function expansions. Ark. Mat. 17 (1979), 139–151.Google Scholar
[8] Folland, G. B., Harmonic Analysis in Phase Space. Princeton University Press, Princeton, NJ, 1989.Google Scholar
[9] Görlich, E. and Markett, C., A convolution structure for Laguerre series. Indag. Math. 44 (1982), 161–171.Google Scholar
[10] Hermann, P., Induced representations and hypergroup homomorphisms. Monatsh. Math. 116 (1993), 245–262.Google Scholar
[11] Jewett, R. I., Spaces with an abstract convolution of measures. Adv. Math. 18 (1975), 1–101.Google Scholar
[12] Koornwinder, T., The addition formula for Laguerre polynomials. SIAM J. Math. Anal. 8 (1977), 535–540.Google Scholar
[13] Koornwinder, T., Jacobi functions and analysis of noncompact semisimple Lie groups. In: Special Functions: Group Theoretical Aspects and Applications (Eds. Askey, R. A., et al.), D. Reidel Publishing Company, 1984, 1–85.Google Scholar
[14] Korányi, A., Some applications of Gelfand pairs in classical analysis. In: Harmonic Analysis and Group Representations, Liguori, Naples, 1982, 333–348.Google Scholar
[15] Mackey, G., Representations of locally compact groups I. Ann. Math. 55 (1952), 101–139.Google Scholar
[16] Parthasarathy, K. R., Probability Measures on Metric Spaces. Academic Press, 1967.Google Scholar
[17] Paterson, A. T., Amenability. Math. Surveys and Monographs 29 , Amer. Math. Soc., 1988.Google Scholar
[18] Rösler, M., Convolution algebras which are not necessarily probability preserving. In: Applications of hypergroups and related measure algebras (Summer Research Conference, Seattle, 1993). Contemp. Math. 183 (1995), 299–318.Google Scholar
[19] Rösler, M., On the dual of a commutative signed hypergroup. Manuscripta Math. 88 (1995), 147–163.Google Scholar
[20] Rösler, M., Bessel-type signed hypergroups on R. In: Probability measures on groups XI (Oberwolfach, 1994). World Scientific Publ., Singapore, 1995, 292–304.Google Scholar
[21] Ross, K. A., Centers of hypergroups. Trans. Amer. Math. Soc. 243 (1978), 251–269.Google Scholar
[22] Ross, K. A., Signed hypergroups—a survey. In: Applications of hypergroups and related measure algebras (Summer Research Conference, Seattle, 1993). Contemp. Math. 183 (1995), 319–329.Google Scholar
[23] Spector, R., Mesures invariantes sur les hypergroupes. Trans. Amer. Math. Soc. 239 (1978), 147–166.Google Scholar
[24] Stempak, K., Almost everywhere summability of Laguerre series. Studia Math. (2) 100 (1991), 129–147.Google Scholar
[25] Thangavelu, S., Lectures on Hermite and Laguerre Expansions. Math. Notes 42 , Princeton Univ. Press, Princeton, NJ, 1993.Google Scholar
[26] Trimèche, K., Operateurs de permutation et analyse harmonique associés a des operáteurs aux dérivées partielles. J. Math. Pures Appl. 70 (1991), 1–73.Google Scholar
[27] Voit, M., Duals of subhypergroups and quotients of commutative hypergroups. Math. Z. 210 (1992), 289–304.Google Scholar
[28] Voit, M., A positivity result and normalization of positive convolution structures. Math. Ann. 297 (1993), 677–692.Google Scholar
[29] Voit, M., Substitution of open subhypergroups. Hokkaido Math. J. 23 (1994), 143–183.Google Scholar