Published online by Cambridge University Press: 20 November 2018
If the Hasse invariant of a 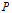 $P$
-divisible group is small enough, then one can construct a canonical subgroup inside its
$P$
-divisible group is small enough, then one can construct a canonical subgroup inside its 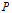 $P$-torsion. We prove that, assuming the existence of a subgroup of adequate height in the
$P$-torsion. We prove that, assuming the existence of a subgroup of adequate height in the 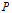 $P$-torsion with high degree, the expected properties of the canonical subgroup can be easily proved, especially the relation between its degree and the Hasse invariant. When one considers a
$P$-torsion with high degree, the expected properties of the canonical subgroup can be easily proved, especially the relation between its degree and the Hasse invariant. When one considers a 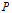 $P$-divisible group with an action of the ring of integers of a (possibly ramified) finite extension of
$P$-divisible group with an action of the ring of integers of a (possibly ramified) finite extension of 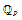 ${{\mathbb{Q}}_{P}}$
, then much more can be said. We define partial Hasse invariants (which are natural in the unramified case, and generalize a construction of Reduzzi and Xiao in the general case), as well as partial degrees. After studying these functions, we compute the partial degrees of the canonical subgroup.
${{\mathbb{Q}}_{P}}$
, then much more can be said. We define partial Hasse invariants (which are natural in the unramified case, and generalize a construction of Reduzzi and Xiao in the general case), as well as partial degrees. After studying these functions, we compute the partial degrees of the canonical subgroup.