Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hofmann, Charles E.
1971.
Specializations of Pascal's theorem on an oval.
Journal of Geometry,
Vol. 1,
Issue. 2,
p.
143.
BARLOTTI, A.
1973.
A Survey of Combinatorial Theory.
p.
1.
Artzy, R.
1973.
A pascal theorem applied to Minkowski geometry.
Journal of Geometry,
Vol. 3,
Issue. 1,
p.
93.
Pellegrino, Giuseppe
1978.
t-Designs associated with non degenerate conics in a Galois plane of odd order.
Journal of Statistical Planning and Inference,
Vol. 2,
Issue. 3,
p.
307.
Barlotti, Adriano
1980.
Combinatorial Mathematics, Optimal Designs and Their Applications.
Vol. 6,
Issue. ,
p.
1.
Mäurer, Helmut
1981.
Geometry — von Staudt’s Point of View.
p.
197.
Amici, O.
and
Casciaro, B.
1983.
Combinatorics '81 in honour of Beniamino Segre, Proceedings of the International Conference on Combinatorial Geometrics and their Applications.
Vol. 78,
Issue. ,
p.
17.
Fernandes, Olga
1984.
On an Oval with the Four Point Pascalian Property.
Canadian Mathematical Bulletin,
Vol. 27,
Issue. 3,
p.
295.
Fernandes, Olga
1985.
On a Baer involution which maps an oval into itself.
Archiv der Mathematik,
Vol. 44,
Issue. 5,
p.
467.
Cherowitzo, William
1986.
On the projectivity of B-ovals.
Journal of Geometry,
Vol. 27,
Issue. 2,
p.
119.
Fernandes, Olga
1993.
On Pascal ovals.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 54,
Issue. 1,
p.
61.
Schröder, Eberhard M.
1995.
Handbook of Incidence Geometry.
p.
945.
Bamberg, John
Harris, Tim
and
Penttila, Tim
2018.
On abstract ovals with Pascalian secant lines.
Journal of Group Theory,
Vol. 21,
Issue. 6,
p.
1051.
Pambuccian, Victor
and
Schacht, Celia
2019.
Geometry in History.
p.
355.
Bamberg, John
and
Penttila, Tim
2023.
Simpler foundations for the hyperbolic plane.
Forum Mathematicum,
Vol. 35,
Issue. 5,
p.
1301.
Biondi, Paola
Durante, Nicola
and
Penttila, Tim
2024.
Harmonic ovals.
Journal of Geometry,
Vol. 115,
Issue. 2,
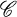 in a projective plane π is a set of points of π such that:
in a projective plane π is a set of points of π such that: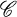 are collinear; this means that a line of π is either a secant of
are collinear; this means that a line of π is either a secant of 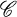 , containing two points of
, containing two points of 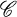 , or a tangent of
, or a tangent of 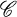 , containing just one point of
, containing just one point of 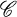 , or a non-secant of
, or a non-secant of 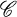 , containing no point of
, containing no point of 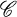 ;
;
