No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let  be an adapted sequence of integrable random variables on the probability space
be an adapted sequence of integrable random variables on the probability space 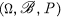 . Let us set
. Let us set  .The following result can be immediately derived from Brown [2]:
.The following result can be immediately derived from Brown [2]:
