Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T15:40:45.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Kloosterman Integrals for GL(3): II

Published online by Cambridge University Press:  20 November 2018

Hervé Jacquet
Hervé Jacquet*
Affiliation:
Department of Mathematics, Columbia University, New York, New York 10027, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G′ be a quasi–split reductive group over a local field F, ƒ′ the characteristic function of a maximal compact subgroup K′ of G′, N′ a maximal unipotent subgroup of G′. We consider the orbits of maximal dimension for the action of N′ × N′ on G′ and the weighted orbital integral of f′ on such an orbit, the weight being a generic character. The resulting integral, we call a Kloosterman integral. A relative version of this construction is to consider a symmetric space S associated to a quasi-split group G, a maximal unipotent subgroup N of G, a maximal compact K of G and the orbits of maximal dimension for the action of N on S. The weighted orbital integral of the characteristic function f of K ∩ S on such an orbit is what we call a relative Kloosterman integral; the weight is an appropriate character of N. We conjecture that a relative Kloosterman integral is actually a Kloosterman integral for an appropriate group G′. We prove the conjecture in a simple case: E is an unramified quadratic extension of F,G is GL(3, E), S is the set of 3 × 3 matrices s such that 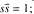the group G′ is then the quasi-split unitary group in three variables.

Keywords

11F3011F7022E50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 6 , 01 December 1992 , pp. 1220 - 1240
Copyright
Copyright © Canadian Mathematical Society 1992

References

[A-C] Arthur, J. and Clozel, L., Simple algebras, base change, and the advanced theory of the trace formula, Annals of Mathematics Studies120, Princeton, 1989.Google Scholar
[Fl] Flicker, Y., Twisted tensors and Euler products, Bulletin de la Société Mathématique de France 116(1988).Google Scholar
[F2] Flicker, Y., Base change trace identity for U(3), Journal d'Analyse Mathématique 52(1989).Google Scholar
[F3] Flicker, Y., On distinguished representations, reine, J. angew. Math.418( 1991 ), 139–172.Google Scholar
[Fr] Friedberg, S., Poincaré series for GL(n): Fourier Expansion, Kloosterman Sums, and Algebro-Geometric Estimates., Math. Z. 196v(1987), 165–188.Google Scholar
[G] Goldfeld, D., Kloosterman zeta functions for GL(n, Z), Proc. Intern. Cong. Math., Berkeley, 1(1986), 417–424.Google Scholar
[H-L-R] Harder, G., Langlands, R.P. and Rapoport, M., Algebraische Zyklen auf Hilbert-Blumenthal-Flàchen, Journal fur Math. 366(1986), 53–120.Google Scholar
[J] Jacquet, H., On the non vanishing of some L—functions, Proc. Indian Acad. Sci. (Math. Sci.), 97(1987), 117–155.Google Scholar
[J-Y] Jacquet, H. and Ye, Y., Une remarque sur le changement de base quadratique, C.R. Acad. Sci. Paris 311(1990), 671–767.Google Scholar
[R] Rogawski, J., Automorphic Representations of Unitary Groups in three variables, Annals of Mathematics Studies (123), Princeton University Press, 1990.Google Scholar
[S] Springer, T.A., Some results on algebraic groups with involutionsin Algebraic groups and Related Topics, Advanced Studies in Mathematics 6, Tokyo (1984), 323–343.Google Scholar
[Y] Ye, Y, Kloosterman integrals and base change for GL(2), J. reine angew. Math. 400(1989), 57–121.Google Scholar