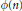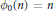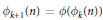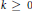Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Germain, Jam
2009.
On the Equation ax ≡ x (mod b).
Integers,
Vol. 9,
Issue. 6,
Ford, Kevin
Konyagin, Sergei V.
and
Luca, Florian
2010.
Prime Chains and Pratt Trees.
Geometric and Functional Analysis,
Vol. 20,
Issue. 5,
p.
1231.
Pollack, Paul
2011.
Two remarks on iterates of Euler’s totient function.
Archiv der Mathematik,
Vol. 97,
Issue. 5,
p.
443.
Pomerance, Carl
2015.
Analytic Number Theory.
p.
321.
Banks, W D
Friedlander, J B
Pomerance, C
and
Shparlinski, I E
2019.
COUNTING INTEGERS WITH A SMOOTH TOTIENT.
The Quarterly Journal of Mathematics,
Vol. 70,
Issue. 4,
p.
1371.
Jiang, Yujiao
Lü, Guangshi
and
Wang, Zhiwei
2022.
Averaged forms of two conjectures of Erdős and Pomerance, and their applications.
Advances in Mathematics,
Vol. 409,
Issue. ,
p.
108592.
Kumar, Arvind
Kumari, Moni
Moree, Pieter
and
Singh, Sujeet Kumar
2023.
Ramanujan-style congruences for prime level.
Mathematische Zeitschrift,
Vol. 303,
Issue. 1,
LEONETTI, PAOLO
and
LUCA, FLORIAN
2024.
ON THE ITERATES OF THE SHIFTED EULER’S FUNCTION.
Bulletin of the Australian Mathematical Society,
Vol. 109,
Issue. 2,
p.
206.
Akande, Agbolade
2024.
The number of preimages of iterates of ϕ and σ.
Journal of Number Theory,
Vol. 259,
Issue. ,
p.
82.