Published online by Cambridge University Press: 20 November 2018
In this paper we shall prove that every finite lattice is isomorphic to a sublattice of the degrees of unsolvability, and that every one of a certain class of finite lattices is isomorphic to an initial segment of degrees.
Acknowledgment. I am grateful to Ralph McKenzie for his assistance in matters of lattice theory.
1. Representation of lattices. The equivalence lattice 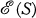 of the set S consists of all equivalence relations on S, ordered by setting θ ≦ θ’ if for all a and b in S, a θ b ⇒ a θ’ b. The least upper bound and greatest lower bound in
of the set S consists of all equivalence relations on S, ordered by setting θ ≦ θ’ if for all a and b in S, a θ b ⇒ a θ’ b. The least upper bound and greatest lower bound in 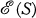 are given by the ⋃ and ⋂ operations:
are given by the ⋃ and ⋂ operations: