Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T13:07:38.551Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theorem Concerning Partitions and its Consequence in the Theory of Lie Algebras

Published online by Cambridge University Press:  20 November 2018

J. W. B. Hughes
J. W. B. Hughes*
Affiliation:
Queen Mary College, London
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the first part of this paper we state and prove a theorem concerning the partition (j; l, i) of an integer j into at most l integers 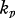, none of which exceed i; l and i being themselves integers, (j; l, i) is thus the number of distinct solutions of the equations

1.1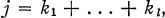

where the 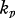satisfy the inequalities

1.2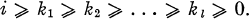

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 698 - 700
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Dickson, L. E., History of the theory of numbers, Vol. 2 (Stechert, New York, 1934).Google Scholar
2. Dynkin, E. B., Maximal sub-groups of the classical groups, Supplement, Amer. Math. Soc. Transi., Ser. 2, 6 (1957), 319.Google Scholar
3. Dynkin, E. B., Some properties of the system of weights of a linear representation of a semisimple Lie group, Dokl. Akad. NaukSSSR (N.S.), 71 (1950), 221.Google Scholar
4. Hughes, J. W. B., Theory of unitary groups, University College, London, Department of Physics Review paper (September, 1965).Google Scholar