Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T21:32:52.839Z Has data issue: false hasContentIssue false
  • English
  • Français

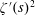Titchmarsh’s Method for the Approximate Functional Equations for $\unicode[STIX]{x1D701}^{\prime }(s)^{2}$, 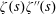$\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 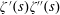$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  09 January 2019

Jun Furuya ,
T. Makoto Minamide  and
Yoshio Tanigawa
Jun Furuya
Affiliation:
Department of Integrated Human Sciences (Mathematics), Hamamatsu University School of Medicine, Handayama 1-20-1, Shizuoka 431-3192, Japan Email: jfuruya@hama-med.ac.jp
T. Makoto Minamide
Affiliation:
Graduate School of Sciences and Technology for Innovation, Yamaguchi University, Yoshida 1677-1, Yamaguchi 753-8512, Japan Email: minamide@yamaguchi-u.ac.jp
Yoshio Tanigawa
Affiliation:
Graduate School of Mathematics, Nagoya University, Furo-cho, Nagoya 464-8602, Japan Email: tanigawa@math.nagoya-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 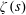$\unicode[STIX]{x1D701}(s)$ be the Riemann zeta function. In 1929, Hardy and Littlewood proved the approximate functional equation for 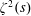$\unicode[STIX]{x1D701}^{2}(s)$ with error term 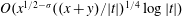$O(x^{1/2-\unicode[STIX]{x1D70E}}((x+y)/|t|)^{1/4}\log |t|)$, where 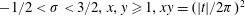$-1/2<\unicode[STIX]{x1D70E}<3/2,x,y\geqslant 1,xy=(|t|/2\unicode[STIX]{x1D70B})^{2}$. Later, in 1938, Titchmarsh improved the error term by removing the factor 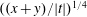$((x+y)/|t|)^{1/4}$. In 1999, Hall showed the approximate functional equations for 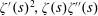$\unicode[STIX]{x1D701}^{\prime }(s)^{2},\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 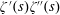$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$ (in the range 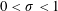$0<\unicode[STIX]{x1D70E}<1$) whose error terms contain the factor 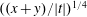$((x+y)/|t|)^{1/4}$. In this paper we remove this factor from these three error terms by using the method of Titchmarsh.

Keywords

derivative of the Riemann zeta functionapproximate functional equationexponential sum

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 6 , December 2019 , pp. 1465 - 1493
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by JSPS KAKENHI: 26400030, 15K17512 and 15K04778.

References

Akatsuka, H., Conditional estimates for error terms related to distribution of zeros of 𝜁 ′ (s) . J. Number Theory 132(2012), 2242–2257. https://doi.org/10.1016/j.jnt.2012.04.012.Google Scholar
Andrews, G. E., Askey, R., and Roy, R., Special functions . Encyclopedia of Mathematics and Its Applications, 71 . Cambridge University Press, 1999.Google Scholar
Aoki, M. and Minamide, M., A zero density estimate of the derivatives of the Riemann zeta function . JANTA 2(2012), 361–375.Google Scholar
Banerjee, D. and Minamide, M., On averages of the error term of a new kind of the divisor problem . J. Math. Anal. Appl. 438(2016), 533–550. https://doi.org/10.1016/j.jmaa.2016.02.013.Google Scholar
Berndt, B. C., The number of zeros for 𝜁(k)(s) . J. London Math. Soc. 2(1970), 577–580. https://doi.org/10.1112/jlms/2.Part_4.577.Google Scholar
Conrey, J. B., The fourth moment of derivatives of Riemann zeta-function . Quart. J. Oxford 39(1988), 21–36. https://doi.org/10.1093/qmath/39.1.21.Google Scholar
Furuya, J., Minamide, M., and Tanigawa, Y., Representations and evaluations of the error term in a certain divisor problem . Math. Slovaca 66(2016), 575–582. https://doi.org/10.1515/ms-2015-0160.Google Scholar
Furuya, J., Minamide, M., and Tanigawa, Y., On a restricted divisor problem . J. Indian Math. Soc. 83(2016), 269–287.Google Scholar
Gonek, S. M., Mean values of the Riemann zeta-function and its derivatives . Invent. Math. 75(1984), 123–141. https://doi.org/10.1007/BF01403094.Google Scholar
Hall, R. R., The behaviour of the Riemann zeta-function on the critical line . Mathematika 46(1999), 281–313. https://doi.org/10.1112/S0025579300007762.Google Scholar
Hardy, G. H. and Littlewood, J. E., The approximate functional equation in the theory of the zeta-functions, with applications to the divisor-problems of Dirichlet and Piltz . Proc. London Math. Soc. (2) 21(1923), 39–74. https://doi.org/10.1112/plms/s2-21.1.39.Google Scholar
Hardy, G. H. and Littlewood, J. E., The approximate functional equations for 𝜁(s) and 𝜁2(s) . Proc. London Math. Soc. (2) 29(1929), 81–97. https://doi.org/10.1112/plms/s2-29.1.81.Google Scholar
Heath-Brown, D. R., The fourth power moment of the Riemann zeta-function . Proc. London Math. Soc. (3) 38(1979), 385–422. https://doi.org/10.1112/plms/s3-38.3.385.Google Scholar
Ingham, A. E., Mean-value theorems in the theory of the Riemann zeta-function . Proc. London Math. Soc. 27(1926), 273–300.Google Scholar
Ivić, A., The Riemann zeta-function . Wiley, New York, 1985.Google Scholar
Levinson, N. and Montgomery, H. L., Zeros of derivatives of the Riemann zeta-functions . Acta Math. 133(1974), 49–65. https://doi.org/10.1007/BF02392141.Google Scholar
Minamide, M., On the truncated Voronoï formula for the derivative of the Riemann zeta function . Indian J. Math. 55(2013), 325–352.Google Scholar
Speiser, A., Geometrisches zur Riemann Zetafuncktion . Math. Ann. 110(1934), 514–521. https://doi.org/10.1007/BF01448042.Google Scholar
Spira, R., Zero-free regions of 𝜁(k)(s) . J. London Math. Soc. 40(1965), 677–682. https://doi.org/10.1112/jlms/s1-40.1.677.Google Scholar
Spira, R., Another zero-free region for 𝜁(k)(s) . Proc. Amer. Math. Soc. 26(1970), 246–247.Google Scholar
Spira, R., Zeros of 𝜁 ′ (s) and the Riemann hypothesis . Illinois J. Math. 17(1973), 147–152.Google Scholar
Titchmarsh, E. C., The approximate functional equation for 𝜁2(s) . Quart. J. Math. 9(1938), 109–114.Google Scholar
Titchmarsh, E. C., The theory of the Riemann zeta-function, Second edition. Revised by D. R. Heath-Brown, Oxford University Press, New York, 1986.Google Scholar