Published online by Cambridge University Press: 20 November 2018
Soit 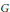 $G$ le groupe
$G$ le groupe 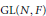 $\text{GL}\,\left( N,\,F \right)$, où
$\text{GL}\,\left( N,\,F \right)$, où 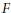 $F$ est un corps localement compact et non archimédien. En utilisant la théorie des types simples de Bushnell et Kutzko, ainsi qu'une idée originale d'Henniart, nous construisons des pseudo-coefficients explicites pour les représentations de la série discrète de
$F$ est un corps localement compact et non archimédien. En utilisant la théorie des types simples de Bushnell et Kutzko, ainsi qu'une idée originale d'Henniart, nous construisons des pseudo-coefficients explicites pour les représentations de la série discrète de 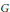 $G$. Comme application, nous en déduisons des formules inédites pour la valeur du charactère d'Harish- Chandra de certaines telles représentations en certainséléments elliptiques réguliers.
$G$. Comme application, nous en déduisons des formules inédites pour la valeur du charactère d'Harish- Chandra de certaines telles représentations en certainséléments elliptiques réguliers.