Article contents
Umbilical Submanifolds of Sn × R
Published online by Cambridge University Press: 20 November 2018
Abstract
We give a complete classification of umbilical submanifolds of arbitrary dimension and codimension of 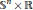 ${{\mathbb{S}}^{n}}\,\times \,\mathbb{R}$, extending the classification of umbilical surfaces in
${{\mathbb{S}}^{n}}\,\times \,\mathbb{R}$, extending the classification of umbilical surfaces in 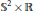 ${{\mathbb{S}}^{2}}\times \mathbb{R}$ by Souam and Toubiana as well as the local description of umbilical hypersurfaces in
${{\mathbb{S}}^{2}}\times \mathbb{R}$ by Souam and Toubiana as well as the local description of umbilical hypersurfaces in 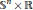 ${{\mathbb{S}}^{n}}\,\times \,\mathbb{R}$ by Van der Veken and Vrancken. We prove that, besides small spheres in a slice, up to isometries of the ambient space they come in a two-parameter family of rotational submanifolds whose substantial codimension is either one or two and whose profile is a curve in a totally geodesic
${{\mathbb{S}}^{n}}\,\times \,\mathbb{R}$ by Van der Veken and Vrancken. We prove that, besides small spheres in a slice, up to isometries of the ambient space they come in a two-parameter family of rotational submanifolds whose substantial codimension is either one or two and whose profile is a curve in a totally geodesic 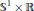 ${{\mathbb{S}}^{1}}\times \mathbb{R}$ or
${{\mathbb{S}}^{1}}\times \mathbb{R}$ or 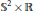 ${{\mathbb{S}}^{2}}\times \mathbb{R}$, respectively, the former case arising in a one-parameter family. All of them are diffeomorphic to a sphere, except for a single element that is diffeomorphic to Euclidean space. We obtain explicit parametrizations of all such submanifolds. We also study more general classes of submanifolds of
${{\mathbb{S}}^{2}}\times \mathbb{R}$, respectively, the former case arising in a one-parameter family. All of them are diffeomorphic to a sphere, except for a single element that is diffeomorphic to Euclidean space. We obtain explicit parametrizations of all such submanifolds. We also study more general classes of submanifolds of 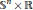 ${{\mathbb{S}}^{n}}\times \mathbb{R}$ and
${{\mathbb{S}}^{n}}\times \mathbb{R}$ and 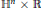 ${{\mathbb{H}}^{n}}\times \mathbb{R}$. In particular, we give a complete description of all submanifolds in those product spaces for which the tangent component of a unit vector field spanning the factor
${{\mathbb{H}}^{n}}\times \mathbb{R}$. In particular, we give a complete description of all submanifolds in those product spaces for which the tangent component of a unit vector field spanning the factor 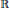 $\mathbb{R}$ is an eigenvector of all shape operators. We show that surfaces with parallel mean curvature vector in
$\mathbb{R}$ is an eigenvector of all shape operators. We show that surfaces with parallel mean curvature vector in 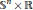 ${{\mathbb{S}}^{n}}\times \mathbb{R}$ and
${{\mathbb{S}}^{n}}\times \mathbb{R}$ and 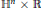 ${{\mathbb{H}}^{n}}\times \mathbb{R}$ having this property are rotational surfaces, and use this fact to improve some recent results by Alencar, do Carmo, and Tribuzy. We also obtain a Dajczer-type reduction of codimension theorem for submanifolds of
${{\mathbb{H}}^{n}}\times \mathbb{R}$ having this property are rotational surfaces, and use this fact to improve some recent results by Alencar, do Carmo, and Tribuzy. We also obtain a Dajczer-type reduction of codimension theorem for submanifolds of 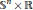 ${{\mathbb{S}}^{n}}\times \mathbb{R}$ and
${{\mathbb{S}}^{n}}\times \mathbb{R}$ and 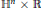 ${{\mathbb{H}}^{n}}\times \mathbb{R}$.
${{\mathbb{H}}^{n}}\times \mathbb{R}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
- 15
- Cited by


