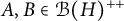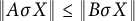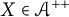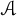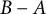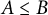1 Introduction
Recently, in [Reference Molnár9], the author studied the question of when the norm of a given mean, on the positive cone of an operator algebra, determines the Löwner order. As explained clearly in the introduction by the author, this problem is of relevance to the study of maps between positive cones of operator algebras that preserve a given norm of a given operator mean. Such a study has received considerable attention, as can be seen, for example, in [Reference Molnár5–Reference Molnár8]. The motivation of such investigations comes, first, from the study of norm additive maps or spectrally multiplicative maps, and second, from the study of the structure of certain quantum mechanical symmetry transformations relating to divergences.
Let us recall that a binary operation
![]() $\sigma $
on
$\sigma $
on
![]() $\mathcal B(H)^{++}$
is called a Kubo–Ando connection if it satisfies the following properties:
$\mathcal B(H)^{++}$
is called a Kubo–Ando connection if it satisfies the following properties:
-
(i) If
 $A \leq C$
and
$A \leq C$
and
 $B \leq D$
, then
$B \leq D$
, then
 $ A \sigma B \leq C \sigma D $
.
$ A \sigma B \leq C \sigma D $
. -
(ii)
 $ C (A \sigma B) C \leq (CAC) \sigma (CBC) $
.
$ C (A \sigma B) C \leq (CAC) \sigma (CBC) $
. -
(iii) If
 $ A_n \downarrow A$
and
$ A_n \downarrow A$
and
 $ B_n \downarrow B $
, then
$ B_n \downarrow B $
, then
 $ A_n \sigma B_n \downarrow A \sigma B$
.Footnote
1
$ A_n \sigma B_n \downarrow A \sigma B$
.Footnote
1
A Kubo–Ando mean is a Kubo–Ando connection with the normalization condition
![]() $I\sigma I=I$
. The most fundamental connections are:
$I\sigma I=I$
. The most fundamental connections are:
-
• the sum
 $(A,B)\mapsto A+B$
,
$(A,B)\mapsto A+B$
, -
• the parallel sum
 $(A,B)\mapsto A:B=\left (A^{-1}+B^{-1}\right )^{-1}$
,
$(A,B)\mapsto A:B=\left (A^{-1}+B^{-1}\right )^{-1}$
, -
• the geometric mean
 $$\begin{align*}(A,B)\mapsto A\sharp B=A^{{\scriptscriptstyle \frac{1}{2}}}\,\left(A^{{\scriptscriptstyle -\frac{1}{2}}}BA^{{\scriptscriptstyle -\frac{1}{2}}}\right)^{{\scriptscriptstyle \frac{1}{2}}}A^{{\scriptscriptstyle \frac{1}{2}}}.\end{align*}$$
$$\begin{align*}(A,B)\mapsto A\sharp B=A^{{\scriptscriptstyle \frac{1}{2}}}\,\left(A^{{\scriptscriptstyle -\frac{1}{2}}}BA^{{\scriptscriptstyle -\frac{1}{2}}}\right)^{{\scriptscriptstyle \frac{1}{2}}}A^{{\scriptscriptstyle \frac{1}{2}}}.\end{align*}$$
A function
![]() $f:(0,\infty )\to (0,\infty )$
is said to be operator monotone if
$f:(0,\infty )\to (0,\infty )$
is said to be operator monotone if
![]() $\sum _{i=1}^nf(a_i)P_i\le \sum _{j=1}^mf(b_j)Q_j$
whenever
$\sum _{i=1}^nf(a_i)P_i\le \sum _{j=1}^mf(b_j)Q_j$
whenever
![]() $\sum _{i=1}^na_iP_i\le \sum _{j=1}^mb_jQ_j$
, where
$\sum _{i=1}^na_iP_i\le \sum _{j=1}^mb_jQ_j$
, where
![]() $a_i,b_j>0$
, and the projections
$a_i,b_j>0$
, and the projections
![]() $P_i$
,
$P_i$
,
![]() $Q_j$
satisfy
$Q_j$
satisfy
![]() $\sum _{i=1}^nP_i=\sum _{j=1}^mQ_j=I$
. Such a function is automatically continuous, monotonic increasing, and concave. For an operator-monotone function f, one has
$\sum _{i=1}^nP_i=\sum _{j=1}^mQ_j=I$
. Such a function is automatically continuous, monotonic increasing, and concave. For an operator-monotone function f, one has
![]() $f(A)\le f(B)$
whenever
$f(A)\le f(B)$
whenever
![]() $A,B\in \mathcal B(H)^{++}$
and
$A,B\in \mathcal B(H)^{++}$
and
![]() $A\le B$
. It is easy to see that the class of operator-monotone functions is closed under addition and multiplication by positive real numbers. The transpose
$A\le B$
. It is easy to see that the class of operator-monotone functions is closed under addition and multiplication by positive real numbers. The transpose
![]() $f^\circ $
of the operator-monotone function f, defined by
$f^\circ $
of the operator-monotone function f, defined by
![]() $f^\circ (x):=xf(x^{-1})$
, is again operator-monotone.
$f^\circ (x):=xf(x^{-1})$
, is again operator-monotone.
Let
![]() $\sigma $
be a Kubo–Ando connection on
$\sigma $
be a Kubo–Ando connection on
![]() $\mathcal B(H)^{++}$
. In the proof of [Reference Kubo and Ando4, Theorem 3.2], it is shown that the function defined on
$\mathcal B(H)^{++}$
. In the proof of [Reference Kubo and Ando4, Theorem 3.2], it is shown that the function defined on
![]() $(0,\infty )$
by
$(0,\infty )$
by
![]() $x\mapsto I\sigma (xI)$
has the form
$x\mapsto I\sigma (xI)$
has the form
![]() $x\mapsto f(x)\,I$
for some operator-monotone function f, and it is further shown that
$x\mapsto f(x)\,I$
for some operator-monotone function f, and it is further shown that
![]() $f(B)=I\sigma B$
for every
$f(B)=I\sigma B$
for every
![]() $B\in \mathcal B(H)^{++}$
. This gives
$B\in \mathcal B(H)^{++}$
. This gives
for every
![]() $A,B\in \mathcal B(H)^{++}$
. The function f is called the representing function of
$A,B\in \mathcal B(H)^{++}$
. The function f is called the representing function of
![]() $\sigma $
.
$\sigma $
.
We recall that operator-monotone functions correspond to positive finite Borel measures on
![]() $[0,\infty ]$
Footnote
2
by Löwner’s theorem (see [Reference Donoghue2]): To every operator-monotone function, f corresponds a unique positive and finite Borel measure m on
$[0,\infty ]$
Footnote
2
by Löwner’s theorem (see [Reference Donoghue2]): To every operator-monotone function, f corresponds a unique positive and finite Borel measure m on
![]() $[0,\infty ]$
such that
$[0,\infty ]$
such that
 $$ \begin{align} f(x)&=\,\int_{[0,\infty]}\frac{x(1+t)}{x+t}\,\mathrm{d}m(t)\\&=\,m(\{0\})\,+\,x\,m(\{\infty\})\,+\,\int_{(0,\infty)}\frac{1+t}{t}(t:x)\,\mathrm{d}m(t)\quad(x>0).\nonumber \end{align} $$
$$ \begin{align} f(x)&=\,\int_{[0,\infty]}\frac{x(1+t)}{x+t}\,\mathrm{d}m(t)\\&=\,m(\{0\})\,+\,x\,m(\{\infty\})\,+\,\int_{(0,\infty)}\frac{1+t}{t}(t:x)\,\mathrm{d}m(t)\quad(x>0).\nonumber \end{align} $$
It is easy to see that
![]() $f(0+)=m(\{0\})$
and
$f(0+)=m(\{0\})$
and
![]() $f^\circ (0+)=m(\{\infty \})$
.
$f^\circ (0+)=m(\{\infty \})$
.
Let
![]() $f:(0,\infty )\to (0,\infty )$
be an operator-monotone function, and let m be the positive and finite Borel measure on
$f:(0,\infty )\to (0,\infty )$
be an operator-monotone function, and let m be the positive and finite Borel measure on
![]() $[0,\infty ]$
associated with f via Löwner’s theorem by (1). The binary operation
$[0,\infty ]$
associated with f via Löwner’s theorem by (1). The binary operation
![]() $\sigma _f$
defined on
$\sigma _f$
defined on
![]() $\mathcal B(H)^{++}$
by
$\mathcal B(H)^{++}$
by
satisfies conditions (i) and (ii) of the definition of a Kubo–Ando connection. Moreover,
 $$\begin{align*}I\sigma_f A&= \,f(0+)\,I+f^\circ(0+)\,A\,+\,\int_{(0,\infty)}\frac{1+t}{t}(tI:A)\,\mathrm{d}m(t)\\&=\,\int_{[0,\infty]}A(1+t)(t{I}+A)^{-1}\,\mathrm{d}m(t)\,=\,f(A)\end{align*}$$
$$\begin{align*}I\sigma_f A&= \,f(0+)\,I+f^\circ(0+)\,A\,+\,\int_{(0,\infty)}\frac{1+t}{t}(tI:A)\,\mathrm{d}m(t)\\&=\,\int_{[0,\infty]}A(1+t)(t{I}+A)^{-1}\,\mathrm{d}m(t)\,=\,f(A)\end{align*}$$
for every
![]() $A\in \mathcal B(H)^{++}$
, and therefore
$A\in \mathcal B(H)^{++}$
, and therefore
for every
![]() $A,B\in \mathcal B(H)^{++}$
. Using the fact that a continuous real-valued function is SOT (strong operator topology) continuous on bounded sets of self-adjoint operators (see [Reference Kadison and Ringrose3, Proposition 5.3.2, p. 327]), it follows that if
$A,B\in \mathcal B(H)^{++}$
. Using the fact that a continuous real-valued function is SOT (strong operator topology) continuous on bounded sets of self-adjoint operators (see [Reference Kadison and Ringrose3, Proposition 5.3.2, p. 327]), it follows that if
![]() $A_n\downarrow A$
and
$A_n\downarrow A$
and
![]() $B_n\downarrow B$
in
$B_n\downarrow B$
in
![]() $\mathcal B(H)^{++}$
, then
$\mathcal B(H)^{++}$
, then
![]() $A_n\sigma _f B_n\downarrow A\sigma _f B$
. This shows that
$A_n\sigma _f B_n\downarrow A\sigma _f B$
. This shows that
![]() $\sigma _f$
is a Kubo–Ando connection on
$\sigma _f$
is a Kubo–Ando connection on
![]() $\mathcal B(H)^{++}$
.
$\mathcal B(H)^{++}$
.
We further recall that if
![]() $\sigma $
is a Kubo–Ando connection with representing function f, then the representing function of the “reversed” Kubo–Ando connection
$\sigma $
is a Kubo–Ando connection with representing function f, then the representing function of the “reversed” Kubo–Ando connection
![]() ${(A,B)\mapsto B\sigma A}$
is the transpose
${(A,B)\mapsto B\sigma A}$
is the transpose
![]() $f^\circ $
. The Kubo–Ando connection is said to be symmetric if it coincides with its reverse, i.e., a Kubo–Ando connection is symmetric if and only if the representing function f satisfies
$f^\circ $
. The Kubo–Ando connection is said to be symmetric if it coincides with its reverse, i.e., a Kubo–Ando connection is symmetric if and only if the representing function f satisfies
![]() $f=f^\circ $
as shown in [Reference Kubo and Ando4, Corollary 4.2]. The Kubo–Ando means are precisely the Kubo–Ando connections whose representing functions satisfy the normalizing condition
$f=f^\circ $
as shown in [Reference Kubo and Ando4, Corollary 4.2]. The Kubo–Ando means are precisely the Kubo–Ando connections whose representing functions satisfy the normalizing condition
![]() $f(1)=1$
.
$f(1)=1$
.
The most fundamental Kubo–Ando means are the power means which correspond to the operator-monotone functions
 $$\begin{align*}f_{{\scriptscriptstyle p}}(t):=\begin{cases} \left(\dfrac{1+t^p}{2}\right)^{\frac{1}{p}}, & \mbox{if } -1\le p\le 1,\ p\neq 0, \\ \sqrt{t}, & \mbox{if } p=0. \end{cases}\end{align*}$$
$$\begin{align*}f_{{\scriptscriptstyle p}}(t):=\begin{cases} \left(\dfrac{1+t^p}{2}\right)^{\frac{1}{p}}, & \mbox{if } -1\le p\le 1,\ p\neq 0, \\ \sqrt{t}, & \mbox{if } p=0. \end{cases}\end{align*}$$
The principal cases
![]() $f_{{\scriptscriptstyle 0}}(t)=\sqrt {t}$
,
$f_{{\scriptscriptstyle 0}}(t)=\sqrt {t}$
,
![]() $f_{{\scriptscriptstyle -1}}(t)=\frac {2t}{1+t}$
, and
$f_{{\scriptscriptstyle -1}}(t)=\frac {2t}{1+t}$
, and
![]() $f_{{\scriptscriptstyle 1}}(t)=\frac {1+t}{2}$
correspond, respectively, to the geometric mean
$f_{{\scriptscriptstyle 1}}(t)=\frac {1+t}{2}$
correspond, respectively, to the geometric mean
![]() $(A,B)\mapsto A\sharp B$
, the harmonic mean
$(A,B)\mapsto A\sharp B$
, the harmonic mean
![]() $(A,B)\mapsto A!B=2(A:B)$
, and the arithmetic mean
$(A,B)\mapsto A!B=2(A:B)$
, and the arithmetic mean
![]() $(A,B)\mapsto A\nabla B=(A+B)/2$
.
$(A,B)\mapsto A\nabla B=(A+B)/2$
.
It is easy to verify that the measure m associated with the arithmetic mean is
![]() $(\delta _{{\scriptscriptstyle 0}}+\delta _{{\scriptscriptstyle \infty }})/2$
and that associated with the harmonic mean is
$(\delta _{{\scriptscriptstyle 0}}+\delta _{{\scriptscriptstyle \infty }})/2$
and that associated with the harmonic mean is
![]() $\delta _{{\scriptscriptstyle 1}}$
, where
$\delta _{{\scriptscriptstyle 1}}$
, where
![]() $\delta _{{\scriptscriptstyle x}}$
denotes the Dirac measure on the point
$\delta _{{\scriptscriptstyle x}}$
denotes the Dirac measure on the point
![]() $x\in [0,\infty ]$
.
$x\in [0,\infty ]$
.

A remark on the domain of definition of a Kubo–Ando connection: We have opted for having
![]() $\mathcal B(H)^{++}$
the defining domain of a Kubo–Ando connection (as opposed to
$\mathcal B(H)^{++}$
the defining domain of a Kubo–Ando connection (as opposed to
![]() $\mathcal B(H)^+$
) in order to obtain fully consistent interchangeable relations in the diagram above. It must be said, however, that this offers no handicap because any Kubo–Ando connection
$\mathcal B(H)^+$
) in order to obtain fully consistent interchangeable relations in the diagram above. It must be said, however, that this offers no handicap because any Kubo–Ando connection
![]() $\sigma $
on
$\sigma $
on
![]() $\mathcal B(H)^{++}$
can be uniquely extended to a binary relation
$\mathcal B(H)^{++}$
can be uniquely extended to a binary relation
![]() $\hat \sigma $
on
$\hat \sigma $
on
![]() $\mathcal B(H)^+$
by setting
$\mathcal B(H)^+$
by setting
![]() $A\hat \sigma B$
equal to
$A\hat \sigma B$
equal to
and it is not hard to show that the extension
![]() $\hat \sigma $
satisfies (i)–(iii) of the definition of a Kubo–Ando connection. Note that the equality
$\hat \sigma $
satisfies (i)–(iii) of the definition of a Kubo–Ando connection. Note that the equality
where f is the representing function associated with
![]() $\sigma $
, holds only on
$\sigma $
, holds only on
![]() $\mathcal B(H)^{++}\times \mathcal B(H)^{+}$
. We further remark that the continuity properties of the function calculus (see [Reference Kadison and Ringrose3, Proposition 5.3.2, p. 327]) imply the following continuity properties of
$\mathcal B(H)^{++}\times \mathcal B(H)^{+}$
. We further remark that the continuity properties of the function calculus (see [Reference Kadison and Ringrose3, Proposition 5.3.2, p. 327]) imply the following continuity properties of
![]() $\hat \sigma $
.
$\hat \sigma $
.
Remark 1
-
(i) The map
(2)is continuous when the domain is equipped with the product of the relative topologies induced by the norm, and the range with the norm topology, and $$ \begin{align}\hat\sigma\,:\,\mathcal B(H)^{++}\times \mathcal B(H)^{+}\,\to\, \mathcal B(H)^{+}\,:\,(A,B)\,\mapsto\, A^{{\scriptscriptstyle \frac{1}{2}}}\,f\left(A^{{\scriptscriptstyle -\frac{1}{2}}}BA^{{\scriptscriptstyle -\frac{1}{2}}}\right)A^{{\scriptscriptstyle \frac{1}{2}}} \end{align} $$
$$ \begin{align}\hat\sigma\,:\,\mathcal B(H)^{++}\times \mathcal B(H)^{+}\,\to\, \mathcal B(H)^{+}\,:\,(A,B)\,\mapsto\, A^{{\scriptscriptstyle \frac{1}{2}}}\,f\left(A^{{\scriptscriptstyle -\frac{1}{2}}}BA^{{\scriptscriptstyle -\frac{1}{2}}}\right)A^{{\scriptscriptstyle \frac{1}{2}}} \end{align} $$
-
(ii) for every
 $\epsilon , R>0$
, the restriction of
$\epsilon , R>0$
, the restriction of
 $\hat \sigma $
to the rectangle is continuous when the domain is equipped with the product of the relative topologies induced by SOT, and the range with SOT.
$\hat \sigma $
to the rectangle is continuous when the domain is equipped with the product of the relative topologies induced by SOT, and the range with SOT. $$\begin{align*}[\epsilon I\,,\,RI]\times[0\,,\,RI]\end{align*}$$
$$\begin{align*}[\epsilon I\,,\,RI]\times[0\,,\,RI]\end{align*}$$
In the sequel, we will not distinguish between
![]() $\sigma $
and
$\sigma $
and
![]() $\hat \sigma $
any further.
$\hat \sigma $
any further.
2 Preliminary considerations
In this section, we collate a list of lemmas and propositions which will prove to be helpful in proving the main result.
Lemma 1 Let
![]() $f:(0, \infty ) \rightarrow (0, \infty ) $
be an operator-monotone function, and let m denote the positive and finite Borel measure associated with f via (1).
$f:(0, \infty ) \rightarrow (0, \infty ) $
be an operator-monotone function, and let m denote the positive and finite Borel measure associated with f via (1).
-
(i) If f is symmetric,
 $\int _{[0,\infty ]}t\,\mathrm {d}m(t)=\int _{[0,\infty ]}t^{-1}\,\mathrm {d}m(t)$
.
$\int _{[0,\infty ]}t\,\mathrm {d}m(t)=\int _{[0,\infty ]}t^{-1}\,\mathrm {d}m(t)$
. -
(ii) For every Borel subset
 $\Delta $
of
$\Delta $
of
 $[0,\infty ]$
satisfying
$[0,\infty ]$
satisfying
 $m(\Delta )>0$
, the function
$m(\Delta )>0$
, the function
 $f_\Delta $
defined on
$f_\Delta $
defined on
 $(0,\infty )$
by
$(0,\infty )$
by  $$\begin{align*}f_\Delta:x\mapsto\int_{\Delta}\frac{x(1+t)}{x+t}\,\mathrm{d}m(t)\end{align*}$$
$$\begin{align*}f_\Delta:x\mapsto\int_{\Delta}\frac{x(1+t)}{x+t}\,\mathrm{d}m(t)\end{align*}$$
is operator-monotone. In particular, if
 $m((0,\infty ))\neq 0$
, the function h defined by
$m((0,\infty ))\neq 0$
, the function h defined by  $$\begin{align*}h(x):=\int_{(0,\infty)}\frac{x(1+t)}{x+t}\,\mathrm{d}m(t)=f(x)-f(0+)-f^\circ(0+) x\quad(x>0)\end{align*}$$
$$\begin{align*}h(x):=\int_{(0,\infty)}\frac{x(1+t)}{x+t}\,\mathrm{d}m(t)=f(x)-f(0+)-f^\circ(0+) x\quad(x>0)\end{align*}$$
is operator-monotone. If f is symmetric, then so is h.
Proof (i) By the Monotone Convergence Theorem, one has that
and since
![]() $f^\circ (x)=xf(1/x)$
, one also gets
$f^\circ (x)=xf(1/x)$
, one also gets
So, if f is symmetric,
![]() $\int _{[0,\infty ]}t\,\mathrm {d}m(t)=\int _{[0,\infty ]}t^{-1}\,\mathrm {d}m(t)$
.
$\int _{[0,\infty ]}t\,\mathrm {d}m(t)=\int _{[0,\infty ]}t^{-1}\,\mathrm {d}m(t)$
.
(ii) If
![]() $\Delta $
is a Borel subset of
$\Delta $
is a Borel subset of
![]() $[0,\infty ]$
satisfying
$[0,\infty ]$
satisfying
![]() $m(\Delta )>0$
, the function on the Borel
$m(\Delta )>0$
, the function on the Borel
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $[0,\infty ]$
defined by
$[0,\infty ]$
defined by
![]() $m_\Delta :\Omega \mapsto m(\Delta \cap \Omega )$
is a positive finite Borel measure and therefore
$m_\Delta :\Omega \mapsto m(\Delta \cap \Omega )$
is a positive finite Borel measure and therefore
is operator-monotone.
Setting
![]() $\Delta =(0,\infty )$
, one obtains that
$\Delta =(0,\infty )$
, one obtains that
is operator-monotone. Since
![]() $m(\{0\})=f(0+)$
and
$m(\{0\})=f(0+)$
and
![]() $m(\{\infty \})=f^\circ (0+)$
,
$m(\{\infty \})=f^\circ (0+)$
,
follows. It is easy to verify that if f is symmetric, so is h.
Let
![]() $X\in \mathcal B(H)$
be self-adjoint and let
$X\in \mathcal B(H)$
be self-adjoint and let
![]() $\Delta $
denote the spectrum of X. The classical measurable function calculus asserts that there exists a
$\Delta $
denote the spectrum of X. The classical measurable function calculus asserts that there exists a
![]() $\ast $
-isomorphism
$\ast $
-isomorphism
![]() $\Phi $
from the Banach algebra
$\Phi $
from the Banach algebra
![]() $L^{\infty }(\Delta ,B(\Delta ),\mu )$
into the abelian von Neumann subalgebra of
$L^{\infty }(\Delta ,B(\Delta ),\mu )$
into the abelian von Neumann subalgebra of
![]() $\mathcal B(H)$
generated by X and I, where
$\mathcal B(H)$
generated by X and I, where
![]() $B(\Delta )$
is the Borel
$B(\Delta )$
is the Borel
![]() $\sigma $
-algebra in
$\sigma $
-algebra in
![]() $\Delta $
, and
$\Delta $
, and
![]() $\mu $
is the composition of any faithful normal positive weight on
$\mu $
is the composition of any faithful normal positive weight on
![]() $\mathcal B(H)$
with the spectral measure associated with X. We recall that
$\mathcal B(H)$
with the spectral measure associated with X. We recall that
![]() $\Phi $
is an isometry, preserves suprema/infima of monotone sequences, and maps the continuous functions on
$\Phi $
is an isometry, preserves suprema/infima of monotone sequences, and maps the continuous functions on
![]() $\Delta $
onto the C*-subalgebra of
$\Delta $
onto the C*-subalgebra of
![]() $\mathcal B(H)$
generated by X and I. Denote by
$\mathcal B(H)$
generated by X and I. Denote by
![]() $\Gamma (X)$
the range of
$\Gamma (X)$
the range of
![]() $\Phi $
. Recall that a lower semicontinuous function
$\Phi $
. Recall that a lower semicontinuous function
![]() $f:\Omega \to [0,1]$
, where
$f:\Omega \to [0,1]$
, where
![]() $\Omega $
is a metrizable space, is the pointwise limit of an increasing sequence of continuous functions (see, for example, [Reference Willard10, Problem 7K, p. 49]). Let
$\Omega $
is a metrizable space, is the pointwise limit of an increasing sequence of continuous functions (see, for example, [Reference Willard10, Problem 7K, p. 49]). Let
![]() $\Gamma _1(X)\subset \Gamma (X)$
denote the image under
$\Gamma _1(X)\subset \Gamma (X)$
denote the image under
![]() $\Phi $
of the set of all bounded lower semicontinuous functions on
$\Phi $
of the set of all bounded lower semicontinuous functions on
![]() $\Delta $
. In particular,
$\Delta $
. In particular,
![]() $\Phi (\chi _{{ }_{{\scriptscriptstyle J}}})\in \Gamma _1(X)$
whenever J is an open subset of
$\Phi (\chi _{{ }_{{\scriptscriptstyle J}}})\in \Gamma _1(X)$
whenever J is an open subset of
![]() $\Delta $
. For the purpose of this paper, such a projection is shortly referred to as a “
$\Delta $
. For the purpose of this paper, such a projection is shortly referred to as a “
![]() $\Gamma _1$
-spectral projection of X.”
$\Gamma _1$
-spectral projection of X.”
Lemma 2 Let
![]() $\sigma $
be a Kubo–Ando connection. For
$\sigma $
be a Kubo–Ando connection. For
![]() $A,B\in \mathcal B(H)^{++}$
, let
$A,B\in \mathcal B(H)^{++}$
, let
![]() $\mathcal A$
denote the C*-subalgebra of
$\mathcal A$
denote the C*-subalgebra of
![]() $\mathcal B(H)$
generated by
$\mathcal B(H)$
generated by
![]() $B-A$
and I. If
$B-A$
and I. If
![]() $ \left \| A \sigma T \right \| \leq \left \| B \sigma T \right \| $
holds for all
$ \left \| A \sigma T \right \| \leq \left \| B \sigma T \right \| $
holds for all
![]() ${ T \in \mathcal {A}^{++} }$
, then
${ T \in \mathcal {A}^{++} }$
, then
![]() $ \left \| A \sigma T \right \| \leq \left \| B \sigma T \right \| $
holds for all positive
$ \left \| A \sigma T \right \| \leq \left \| B \sigma T \right \| $
holds for all positive
![]() $T\in \Gamma _1(B-A)$
.
$T\in \Gamma _1(B-A)$
.
Proof Let us first recall the general fact that whenever
![]() $(T_\gamma )$
is an SOT-convergent net of positive operators, bounded from above by its SOT-limit T, then the net of norms
$(T_\gamma )$
is an SOT-convergent net of positive operators, bounded from above by its SOT-limit T, then the net of norms
![]() $\left (\Vert T_\gamma \Vert \right )$
is convergent to
$\left (\Vert T_\gamma \Vert \right )$
is convergent to
![]() $\Vert T\Vert $
.
$\Vert T\Vert $
.
Invoking the continuity of
![]() $\sigma $
w.r.t. the norm (as mentioned in the introduction), and since
$\sigma $
w.r.t. the norm (as mentioned in the introduction), and since
![]() $\mathcal A^{++}$
is norm-dense in
$\mathcal A^{++}$
is norm-dense in
![]() $\mathcal A^+$
, it can be seen that the hypothesis implies that
$\mathcal A^+$
, it can be seen that the hypothesis implies that
![]() $ \left \| A\sigma T \right \| \le \left \| B\sigma T \right \| $
holds for every
$ \left \| A\sigma T \right \| \le \left \| B\sigma T \right \| $
holds for every
![]() $T\in \mathcal A^+$
.
$T\in \mathcal A^+$
.
Let
![]() $X:=B-A$
. Let
$X:=B-A$
. Let
![]() $(\Delta ,B(\Delta ),\mu )$
be the measure space associated with X, i.e.,
$(\Delta ,B(\Delta ),\mu )$
be the measure space associated with X, i.e.,
![]() $\Delta $
is the spectrum of X,
$\Delta $
is the spectrum of X,
![]() $B(\Delta )$
is the Borel
$B(\Delta )$
is the Borel
![]() $\sigma $
-algebra in
$\sigma $
-algebra in
![]() $\Delta $
, and
$\Delta $
, and
![]() $\mu $
is the composition of any faithful normal positive weight on
$\mu $
is the composition of any faithful normal positive weight on
![]() $\mathcal B(H)$
with the spectral measure associated with X. Let
$\mathcal B(H)$
with the spectral measure associated with X. Let
![]() $\Phi $
be the
$\Phi $
be the
![]() $\ast $
-isomorphism from the Banach algebra
$\ast $
-isomorphism from the Banach algebra
![]() $L^{\infty }(\Delta ,B(\Delta ),\mu )$
into the abelian von Neumann subalgebra of
$L^{\infty }(\Delta ,B(\Delta ),\mu )$
into the abelian von Neumann subalgebra of
![]() $\mathcal B(H)$
generated by X and I.
$\mathcal B(H)$
generated by X and I.
Fix a positive
![]() $T\in \Gamma _1(X)$
. We want to show that
$T\in \Gamma _1(X)$
. We want to show that
![]() $ \left \| A \sigma T \right \| \leq \left \| B \sigma T \right \| $
. Let f be a bounded lower semicontinuous function on
$ \left \| A \sigma T \right \| \leq \left \| B \sigma T \right \| $
. Let f be a bounded lower semicontinuous function on
![]() $\Delta $
satisfying
$\Delta $
satisfying
![]() $\Phi (f)=T$
. There exists a sequence
$\Phi (f)=T$
. There exists a sequence
![]() $(f_n)$
of continuous functions on
$(f_n)$
of continuous functions on
![]() $\Delta $
such that
$\Delta $
such that
![]() $f_n(x)\uparrow f(x)$
as
$f_n(x)\uparrow f(x)$
as
![]() $n\uparrow \infty $
for every
$n\uparrow \infty $
for every
![]() $x\in \Delta $
. Without loss of generality, we can assume that
$x\in \Delta $
. Without loss of generality, we can assume that
![]() $0\le f_n(x)$
for every
$0\le f_n(x)$
for every
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $x\in \Delta $
, i.e., we can suppose that
$x\in \Delta $
, i.e., we can suppose that
![]() $\Phi (f_n)\in \mathcal A^+$
. Applying (ii) of Remark 1, one obtains
$\Phi (f_n)\in \mathcal A^+$
. Applying (ii) of Remark 1, one obtains
![]() $A\,\sigma \,\Phi (f_n)\uparrow A\,\sigma \,T$
and
$A\,\sigma \,\Phi (f_n)\uparrow A\,\sigma \,T$
and
![]() $B\,\sigma \,\Phi (f_n)\uparrow B\,\sigma \,T$
as
$B\,\sigma \,\Phi (f_n)\uparrow B\,\sigma \,T$
as
![]() $n\uparrow \infty $
. The observation recalled in the first paragraph of the proof then yields
$n\uparrow \infty $
. The observation recalled in the first paragraph of the proof then yields
In the subsequent lemma, the main ideas can be found in [Reference Chabbabi, Mbekhta and Molnár1, Lemma 11]. We formalize them and present them here for completeness sake.
Proposition 3 For the operators
![]() $ A, B \in \mathcal B(H)^+$
, the following assertions are equivalent:
$ A, B \in \mathcal B(H)^+$
, the following assertions are equivalent:
-
(i)
 $A\le B$
,
$A\le B$
, -
(ii)
 $ \left \| PAP \right \| \leq \left \| PBP \right \| $
for every
$ \left \| PAP \right \| \leq \left \| PBP \right \| $
for every
 $\Gamma _1$
-spectral projection P of
$\Gamma _1$
-spectral projection P of
 $B-A$
,
$B-A$
, -
(iii)
 $\{\lambda \ge 0:\lambda P\le PAP\}\subseteq \{\lambda \ge 0:\lambda P\le PBP\}$
for every
$\{\lambda \ge 0:\lambda P\le PAP\}\subseteq \{\lambda \ge 0:\lambda P\le PBP\}$
for every
 $\Gamma _1$
-spectral projection P of
$\Gamma _1$
-spectral projection P of
 $B-A$
.
$B-A$
.
Proof The assertions (i)
![]() $\Rightarrow $
(ii) and (i)
$\Rightarrow $
(ii) and (i)
![]() $\Rightarrow $
(iii) are trivial.
$\Rightarrow $
(iii) are trivial.
Let us prove that both (ii) and (iii) imply (i). Suppose that
![]() $A\nleq B$
, for contradiction. Then, there exists
$A\nleq B$
, for contradiction. Then, there exists
![]() $\epsilon> 0 $
such that the spectrum of
$\epsilon> 0 $
such that the spectrum of
![]() $B-A$
has a nontrivial intersection with
$B-A$
has a nontrivial intersection with
![]() $(-\infty , -\epsilon )$
. Let
$(-\infty , -\epsilon )$
. Let
![]() $\Delta $
be the intersection of
$\Delta $
be the intersection of
![]() $(-\infty ,-\epsilon )$
with the spectrum of
$(-\infty ,-\epsilon )$
with the spectrum of
![]() $B-A$
, and let
$B-A$
, and let
![]() $ P_\epsilon $
be the (nonzero)
$ P_\epsilon $
be the (nonzero)
![]() $\Gamma _1$
-spectral projection of
$\Gamma _1$
-spectral projection of
![]() $B-A$
associated with the indicator function
$B-A$
associated with the indicator function
![]() $ \chi _{{}_{\scriptscriptstyle \Delta }}$
. Clearly,
$ \chi _{{}_{\scriptscriptstyle \Delta }}$
. Clearly,
![]() $ t\,\chi _{{}_{\scriptscriptstyle \Delta }}(t)\le -\epsilon \, \chi _{{}_{\scriptscriptstyle \Delta }}(t)$
for every
$ t\,\chi _{{}_{\scriptscriptstyle \Delta }}(t)\le -\epsilon \, \chi _{{}_{\scriptscriptstyle \Delta }}(t)$
for every
![]() $t\in \mathbb R$
, and therefore
$t\in \mathbb R$
, and therefore
![]() $P_\epsilon BP_\epsilon -P_\epsilon AP_\epsilon =P_\epsilon (B-A)P_\epsilon \leq -\epsilon P_\epsilon $
. Rearranging the terms, we get
$P_\epsilon BP_\epsilon -P_\epsilon AP_\epsilon =P_\epsilon (B-A)P_\epsilon \leq -\epsilon P_\epsilon $
. Rearranging the terms, we get
(ii)
![]() $\Rightarrow $
(i). It follows, by (3), that
$\Rightarrow $
(i). It follows, by (3), that
![]() $P_\epsilon A P_\epsilon \ge \epsilon P_\epsilon $
, and therefore
$P_\epsilon A P_\epsilon \ge \epsilon P_\epsilon $
, and therefore
![]() $ \left \| P_\epsilon BP_\epsilon \right \| \leq \left \| P_\epsilon (A-\epsilon I)P_\epsilon \right \| = \left \| P_\epsilon AP_\epsilon \right \| - \epsilon $
.
$ \left \| P_\epsilon BP_\epsilon \right \| \leq \left \| P_\epsilon (A-\epsilon I)P_\epsilon \right \| = \left \| P_\epsilon AP_\epsilon \right \| - \epsilon $
.
(iii)
![]() $\Rightarrow $
(i). First, observe that for every
$\Rightarrow $
(i). First, observe that for every
![]() $A\in \mathcal B(H)^+$
and projection P, the supremum of
$A\in \mathcal B(H)^+$
and projection P, the supremum of
![]() $\{\lambda \ge 0:\lambda P\le PAP\}$
is indeed a maximum and is at most equal to
$\{\lambda \ge 0:\lambda P\le PAP\}$
is indeed a maximum and is at most equal to
![]() $\Vert A\Vert $
. Let
$\Vert A\Vert $
. Let
![]() ${\lambda _0:=\max \{\lambda \ge 0:\lambda P_\epsilon \le P_\epsilon A P_\epsilon \}}$
. Then (iii) and (3) imply that
${\lambda _0:=\max \{\lambda \ge 0:\lambda P_\epsilon \le P_\epsilon A P_\epsilon \}}$
. Then (iii) and (3) imply that
![]() $\lambda _0P_\epsilon \le P_\epsilon B P_\epsilon \le P_\epsilon A P_\epsilon -\epsilon P_\epsilon $
, which in turn shows that
$\lambda _0P_\epsilon \le P_\epsilon B P_\epsilon \le P_\epsilon A P_\epsilon -\epsilon P_\epsilon $
, which in turn shows that
![]() $(\lambda _0+\epsilon )P_{\epsilon }\le P_\epsilon A P_\epsilon $
, contradicting the maximality condition of
$(\lambda _0+\epsilon )P_{\epsilon }\le P_\epsilon A P_\epsilon $
, contradicting the maximality condition of
![]() $\lambda _0$
.
$\lambda _0$
.
In the following proposition, the ideas in [Reference Molnár9, Proposition 10] are used to generalize [Reference Molnár9, equation (15)]. This will be of pivotal importance in proving the main result of this paper.
Proposition 4 Let
![]() $X_s\in \mathcal B(H)^+$
,
$X_s\in \mathcal B(H)^+$
,
![]() $s>0$
satisfy
$s>0$
satisfy
![]() $\lim _{s\to \infty }X_s=X$
in norm, and let
$\lim _{s\to \infty }X_s=X$
in norm, and let
![]() $P\in \mathcal B(H)$
be a projection. Then
$P\in \mathcal B(H)$
be a projection. Then
Proof Let
![]() $\varepsilon>0$
. It can easily be verified that
$\varepsilon>0$
. It can easily be verified that
converges to
![]() $( \left \| PXP \right \| +\varepsilon )^{-1} \left \| PXP \right \| <1$
as
$( \left \| PXP \right \| +\varepsilon )^{-1} \left \| PXP \right \| <1$
as
![]() $s\to \infty $
. Therefore, for sufficiently large s,
$s\to \infty $
. Therefore, for sufficiently large s,
so by multiplying both sides of the above by the inverse of
![]() $ ( \left \| PX_sP \right \| +\varepsilon )^{{\scriptscriptstyle -1/2}}P+s^{{\scriptscriptstyle -1/2}}(I-P) $
, the inequality
$ ( \left \| PX_sP \right \| +\varepsilon )^{{\scriptscriptstyle -1/2}}P+s^{{\scriptscriptstyle -1/2}}(I-P) $
, the inequality
![]() $X_s\le ( \left \| PX_sP \right \| +\varepsilon )P+s(I-P)$
is obtained. This implies that
$X_s\le ( \left \| PX_sP \right \| +\varepsilon )P+s(I-P)$
is obtained. This implies that
for sufficiently large s. On the other hand, for every
![]() $s>0$
,
$s>0$
,
and therefore
Combining (4) and (5), for sufficiently large s, it holds that
This proves that
![]() $\lim _{s\to \infty } \left \| X_s + sP \right \| -s = \left \| PXP \right \| $
.
$\lim _{s\to \infty } \left \| X_s + sP \right \| -s = \left \| PXP \right \| $
.
Proposition 5 [Reference Molnár9, Lemma 2] Let
![]() $f:(0, \infty ) \rightarrow (0, \infty ) $
be a nontrivial
$f:(0, \infty ) \rightarrow (0, \infty ) $
be a nontrivial
![]() $($
i.e., not affine
$($
i.e., not affine
![]() $)$
operator-monotone function satisfying
$)$
operator-monotone function satisfying
![]() $f(0+)=0$
, and let
$f(0+)=0$
, and let
![]() $\sigma $
denote the Kubo–Ando connection associated with f via (2). For
$\sigma $
denote the Kubo–Ando connection associated with f via (2). For
![]() $A\in \mathcal B(H)^{++}$
and nonzero projection
$A\in \mathcal B(H)^{++}$
and nonzero projection
![]() $P\in \mathcal B(H)$
,
$P\in \mathcal B(H)$
,
 $$\begin{align*}\left\| A\sigma P \right\| =f^\circ\left(\frac{1}{\max\{\lambda\ge0:\lambda P\le PA^{-1}P\}}\right).\end{align*}$$
$$\begin{align*}\left\| A\sigma P \right\| =f^\circ\left(\frac{1}{\max\{\lambda\ge0:\lambda P\le PA^{-1}P\}}\right).\end{align*}$$
3 Results
Theorem 6 Let
![]() $\sigma $
be a nontrivial symmetric Kubo–Ando connection on
$\sigma $
be a nontrivial symmetric Kubo–Ando connection on
![]() $\mathcal B(H)^{++}$
. Then, for every
$\mathcal B(H)^{++}$
. Then, for every
![]() $A,B\in \mathcal B(H)^{++}$
,
$A,B\in \mathcal B(H)^{++}$
,
where
![]() $\mathcal A$
equals the C*-subalgebra of
$\mathcal A$
equals the C*-subalgebra of
![]() $\mathcal B(H)$
generated by
$\mathcal B(H)$
generated by
![]() $B-A$
and I.
$B-A$
and I.
Proof The implication
![]() $\Rightarrow $
follows trivially by the monotonicity property of Kubo–Ando connections. We shall show the converse. By Lemma 2, we can suppose that
$\Rightarrow $
follows trivially by the monotonicity property of Kubo–Ando connections. We shall show the converse. By Lemma 2, we can suppose that
![]() $\Vert A\sigma X\Vert \le \Vert B\sigma X\Vert $
holds for every X of the form
$\Vert A\sigma X\Vert \le \Vert B\sigma X\Vert $
holds for every X of the form
![]() $X=s P+tI$
, where P is a
$X=s P+tI$
, where P is a
![]() $\Gamma _1$
-spectral projection of
$\Gamma _1$
-spectral projection of
![]() $B-A$
and
$B-A$
and
![]() $s,t\in \mathbb R^+$
. Let f be the operator-monotone function associated with
$s,t\in \mathbb R^+$
. Let f be the operator-monotone function associated with
![]() $\sigma $
, and let m be the positive and finite Borel measure associated with f by Löwner’s theorem. Let
$\sigma $
, and let m be the positive and finite Borel measure associated with f by Löwner’s theorem. Let
![]() $\alpha =f(0+)=m(\{0\})$
. The proof will be divided in cases.
$\alpha =f(0+)=m(\{0\})$
. The proof will be divided in cases.
Case 1:
![]() $\alpha =0$
. Since
$\alpha =0$
. Since
![]() $f=f^\circ $
is strictly monotonic increasing, this case follows immediately by Propositions 5 and 3. This result was obtained by Molnár in [Reference Molnár9].
$f=f^\circ $
is strictly monotonic increasing, this case follows immediately by Propositions 5 and 3. This result was obtained by Molnár in [Reference Molnár9].
Case 2a:
![]() $\alpha \neq 0$
and
$\alpha \neq 0$
and
![]() $\int _{(0,\infty )}t\,\mathrm {d}m(t)<\infty $
. Let
$\int _{(0,\infty )}t\,\mathrm {d}m(t)<\infty $
. Let
![]() $\gamma :=\int _{(0,\infty )}1+t\,\mathrm {d}m(t)$
. For every
$\gamma :=\int _{(0,\infty )}1+t\,\mathrm {d}m(t)$
. For every
![]() $s,t,\delta>0$
,
$s,t,\delta>0$
,
![]() $A\in \mathcal B(H)^{++}$
and nonzero projection
$A\in \mathcal B(H)^{++}$
and nonzero projection
![]() $P\in \mathcal B(H)$
:
$P\in \mathcal B(H)$
:
 $$ \begin{align*} &\int_{(0,\infty)}\frac{1+t}{t}\left(tA:sP+s\delta I\right)\,\mathrm{d}m(t)\ -\ A\int_{(0,\infty)}1+t\,\mathrm{d}m(t)\\ &\ \quad\qquad\qquad\qquad\qquad=\int_{(0,\infty)}\left(A\left(\left(\frac{tA}{s}+P+\delta I\right)^{-1}(P+\delta I)-I\right)\right)(1+t)\,\mathrm{d}m(t). \end{align*} $$
$$ \begin{align*} &\int_{(0,\infty)}\frac{1+t}{t}\left(tA:sP+s\delta I\right)\,\mathrm{d}m(t)\ -\ A\int_{(0,\infty)}1+t\,\mathrm{d}m(t)\\ &\ \quad\qquad\qquad\qquad\qquad=\int_{(0,\infty)}\left(A\left(\left(\frac{tA}{s}+P+\delta I\right)^{-1}(P+\delta I)-I\right)\right)(1+t)\,\mathrm{d}m(t). \end{align*} $$
Noting that
![]() $\left \Vert A\left (\left (\frac {tA}{s}+P+\delta I\right )^{-1}(P+\delta I)-I\right )\right \Vert $
is a bounded function of s and t, and using the fact that
$\left \Vert A\left (\left (\frac {tA}{s}+P+\delta I\right )^{-1}(P+\delta I)-I\right )\right \Vert $
is a bounded function of s and t, and using the fact that
![]() $\int _{(0,\infty )}1+t\,\mathrm { d}m(t)<\infty $
, it is possible to apply the Dominated Convergence Theorem to infer that
$\int _{(0,\infty )}1+t\,\mathrm { d}m(t)<\infty $
, it is possible to apply the Dominated Convergence Theorem to infer that
converges in norm to
![]() $\gamma \,A$
as
$\gamma \,A$
as
![]() $s\to \infty $
. This implies that
$s\to \infty $
. This implies that
in norm, as
![]() $s\to \infty $
. Noting that
$s\to \infty $
. Noting that
![]() $\beta =m(\{\infty \})=m(\{0\})>0$
and applying Proposition 4, it is deduced that
$\beta =m(\{\infty \})=m(\{0\})>0$
and applying Proposition 4, it is deduced that
Using the fact that
it can be seen that
![]() $\Vert A\sigma (sP+s\delta I)-\beta s\delta I\Vert =\Vert A\sigma (sP+s\delta I)\Vert -\beta s\delta $
. This establishes that
$\Vert A\sigma (sP+s\delta I)-\beta s\delta I\Vert =\Vert A\sigma (sP+s\delta I)\Vert -\beta s\delta $
. This establishes that
So, if
![]() $A, B\in \mathcal B(H)^{++}$
satisfy
$A, B\in \mathcal B(H)^{++}$
satisfy
![]() $ \left \| A\sigma (s P+tI) \right \| \le \left \| B\sigma (s P+tI) \right \| $
for every
$ \left \| A\sigma (s P+tI) \right \| \le \left \| B\sigma (s P+tI) \right \| $
for every
![]() $\Gamma _1$
-spectral projection P of
$\Gamma _1$
-spectral projection P of
![]() $B-A$
and
$B-A$
and
![]() $s,t \in \mathbb R^+$
, it follows that
$s,t \in \mathbb R^+$
, it follows that
![]() $ \left \| PAP \right \| \le \left \| PBP \right \| $
holds for every
$ \left \| PAP \right \| \le \left \| PBP \right \| $
holds for every
![]() $\Gamma _1$
-spectral projection of
$\Gamma _1$
-spectral projection of
![]() $B-A$
. The result follows by Proposition 3.
$B-A$
. The result follows by Proposition 3.
Case 2b:
![]() $\alpha \neq 0$
and
$\alpha \neq 0$
and
![]() $\int _{(0,\infty )}t\,\mathrm {d}m(t)=\infty $
. Denote by
$\int _{(0,\infty )}t\,\mathrm {d}m(t)=\infty $
. Denote by
![]() $\sigma _h$
the (symmetric) Kubo–Ando connection associated with the function
$\sigma _h$
the (symmetric) Kubo–Ando connection associated with the function
![]() $h(x)=f(x)-\alpha -\alpha x$
(see (ii) of Lemma 1). Let
$h(x)=f(x)-\alpha -\alpha x$
(see (ii) of Lemma 1). Let
![]() $m_h$
denote the positive and finite Borel measure associated with h. Then,
$m_h$
denote the positive and finite Borel measure associated with h. Then,
![]() $m_h(\Delta )=m(\Delta \cap (0,\infty ))$
for every Borel subset
$m_h(\Delta )=m(\Delta \cap (0,\infty ))$
for every Borel subset
![]() $\Delta $
of
$\Delta $
of
![]() $[0,\infty ]$
.
$[0,\infty ]$
.
The inequality
holds for every
![]() $\Gamma _1$
-spectral projection P of
$\Gamma _1$
-spectral projection P of
![]() $B-A$
and
$B-A$
and
![]() $s>0$
.
$s>0$
.
Fix an arbitrary
![]() $\Gamma _1$
-spectral projection P of
$\Gamma _1$
-spectral projection P of
![]() $B-A$
. Noting that
$B-A$
. Noting that
![]() $h(sP)=h(s)P$
for every
$h(sP)=h(s)P$
for every
![]() $s>0$
, it can then be deduced that
$s>0$
, it can then be deduced that
i.e.,
![]() $A\sigma _h P$
commutes with P. Thus, (7) yields
$A\sigma _h P$
commutes with P. Thus, (7) yields
 $$ \begin{align*} \Vert \alpha s P\Vert+ \left\| A\sigma_h(sP) \right\| &= \left\| \alpha sP+A\sigma_h (sP) \right\| \\ &\leq\Vert \alpha A+\alpha s P+A\sigma_h(sP)\Vert\\ &\leq \Vert \alpha B+\alpha s P+B\sigma_h(sP)\Vert\\ &\leq \Vert\alpha B\Vert+\Vert\alpha sP\Vert+\Vert B\sigma_h(sP)\Vert, \end{align*} $$
$$ \begin{align*} \Vert \alpha s P\Vert+ \left\| A\sigma_h(sP) \right\| &= \left\| \alpha sP+A\sigma_h (sP) \right\| \\ &\leq\Vert \alpha A+\alpha s P+A\sigma_h(sP)\Vert\\ &\leq \Vert \alpha B+\alpha s P+B\sigma_h(sP)\Vert\\ &\leq \Vert\alpha B\Vert+\Vert\alpha sP\Vert+\Vert B\sigma_h(sP)\Vert, \end{align*} $$
and therefore
for every
![]() $s>0$
.
$s>0$
.
Let
![]() $c_A:= 1/\max \{\lambda \ge 0:\lambda P\le PA^{-1}P\}$
, and let
$c_A:= 1/\max \{\lambda \ge 0:\lambda P\le PA^{-1}P\}$
, and let
![]() $c_B$
be defined similarly. Proposition 5 gives
$c_B$
be defined similarly. Proposition 5 gives
 $$\begin{align*}\Vert A\sigma_h(sP)\Vert =s\Vert (s^{-1}A) \sigma_h P\Vert = s\, h\left(\frac{1}{s\,\max\{\lambda\ge 0:\lambda P\le PA^{-1}P\}}\right)=s\,h\left({c_A}{s^{-1}}\right),\end{align*}$$
$$\begin{align*}\Vert A\sigma_h(sP)\Vert =s\Vert (s^{-1}A) \sigma_h P\Vert = s\, h\left(\frac{1}{s\,\max\{\lambda\ge 0:\lambda P\le PA^{-1}P\}}\right)=s\,h\left({c_A}{s^{-1}}\right),\end{align*}$$
and since
![]() $m_h$
is just the restriction of the measure m (associated with f) to
$m_h$
is just the restriction of the measure m (associated with f) to
![]() $(0,\infty )$
, we obtain
$(0,\infty )$
, we obtain
Similarly,
![]() $\Vert B\sigma _h(sP)\Vert =\int _{(0,\infty )}\frac {sc_B (1+t)}{c_B + st}\, \mathrm {d}m(t)$
, and therefore
$\Vert B\sigma _h(sP)\Vert =\int _{(0,\infty )}\frac {sc_B (1+t)}{c_B + st}\, \mathrm {d}m(t)$
, and therefore
 $$ \begin{align*} \left\| A\sigma_h(sP) \right\| -\Vert B\sigma_h(sP)\Vert &= \int_{(0, \infty)} \frac{sc_A (1+t)}{c_A + st} - \frac{sc_B (1+t)}{{c_B} + st} \, \mathrm{d}m(t)\\ &= (c_A -c_B) \int_{(0, \infty)}\frac{s^{2}t(1+t)}{ (c_A + st)(c_B + st)} \, \mathrm{d}m(t). \end{align*} $$
$$ \begin{align*} \left\| A\sigma_h(sP) \right\| -\Vert B\sigma_h(sP)\Vert &= \int_{(0, \infty)} \frac{sc_A (1+t)}{c_A + st} - \frac{sc_B (1+t)}{{c_B} + st} \, \mathrm{d}m(t)\\ &= (c_A -c_B) \int_{(0, \infty)}\frac{s^{2}t(1+t)}{ (c_A + st)(c_B + st)} \, \mathrm{d}m(t). \end{align*} $$
The Monotone Convergence Theorem implies that as
![]() $s\uparrow \infty $
, the integral increases to
$s\uparrow \infty $
, the integral increases to
![]() $\int _{(0, \infty )} \frac {1}{t} + 1 \, \mathrm {d}m(t)$
. The relation between the two measures m and
$\int _{(0, \infty )} \frac {1}{t} + 1 \, \mathrm {d}m(t)$
. The relation between the two measures m and
![]() $m_h$
, part (i) of Lemma 1, and the hypothesis then yield that
$m_h$
, part (i) of Lemma 1, and the hypothesis then yield that
 $$ \begin{align*} \left\| A\sigma_h(sP) \right\| -\Vert B\sigma_h(sP)\Vert\,\to\ &(c_A-c_B)\int_{(0, \infty)} \frac{1}{t} +1\, \mathrm{d}m(t)\\ &=\,(c_A-c_B)\int_{[0, \infty]} \frac{1}{t}+1 \, \mathrm{d}m_h(t)\\ &=\,(c_A-c_B)\int_{[0, \infty]} t+1 \, \mathrm{d}m_h(t)\\ &=\,(c_A-c_B)\int_{(0, \infty)} {t} +1 \, \mathrm{d}m(t), \end{align*} $$
$$ \begin{align*} \left\| A\sigma_h(sP) \right\| -\Vert B\sigma_h(sP)\Vert\,\to\ &(c_A-c_B)\int_{(0, \infty)} \frac{1}{t} +1\, \mathrm{d}m(t)\\ &=\,(c_A-c_B)\int_{[0, \infty]} \frac{1}{t}+1 \, \mathrm{d}m_h(t)\\ &=\,(c_A-c_B)\int_{[0, \infty]} t+1 \, \mathrm{d}m_h(t)\\ &=\,(c_A-c_B)\int_{(0, \infty)} {t} +1 \, \mathrm{d}m(t), \end{align*} $$
as
![]() $s\uparrow \infty $
. Since
$s\uparrow \infty $
. Since
![]() $\int _{(0, \infty )} {t} + 1 \, \mathrm {d}m(t)=\infty $
, it follows that
$\int _{(0, \infty )} {t} + 1 \, \mathrm {d}m(t)=\infty $
, it follows that
![]() $ c_{A} - c_{B} \leq 0 $
since otherwise one would get a contradiction with (8).
$ c_{A} - c_{B} \leq 0 $
since otherwise one would get a contradiction with (8).
This shows that
for every
![]() $\Gamma _1$
-spectral projection of
$\Gamma _1$
-spectral projection of
![]() $B-A$
, and therefore
$B-A$
, and therefore
![]() $A^{-1}\ge B^{-1}$
by Proposition 3.
$A^{-1}\ge B^{-1}$
by Proposition 3.
Acknowledgment
The authors are grateful to Professor Lajos Molnár (Bolyai Institute and University of Szeged) who introduced the topic and problem to them.