Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T10:42:54.402Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on the Dixmier Conjecture

Part of: Rings and algebras with additional structure Rings and algebras arising under various constructions

Published online by Cambridge University Press:  30 August 2019

V. V. Bavula  and
V. Levandovskyy
V. V. Bavula
Affiliation:
Department of Pure Mathematics, University of Sheffield, Hicks Building, SheffieldS3 7RH, UK Email: v.bavula@sheffield.ac.uk
V. Levandovskyy
Affiliation:
Lehrstuhl D für Mathematik, RWTH Aachen University, 52062 Aachen, Germany Email: Viktor.Levandovskyy@math.rwth-aachen.de
Get access Rights & Permissions [Opens in a new window]

Abstract

The Dixmier Conjecture says that every endomorphism of the (first) Weyl algebra 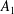$A_{1}$ (over a field of characteristic zero) is an automorphism, i.e., if 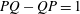$PQ-QP=1$ for some 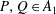$P,Q\in A_{1}$, then 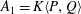$A_{1}=K\langle P,Q\rangle$. The Weyl algebra 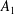$A_{1}$ is a 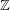$\mathbb{Z}$-graded algebra. We prove that the Dixmier Conjecture holds if the elements 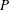$P$ and 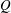$Q$ are sums of no more than two homogeneous elements of 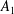$A_{1}$ (there is no restriction on the total degrees of 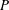$P$ and 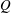$Q$).

Keywords

Weyl algebraDixmier Conjectureautomorphismendomorphisma ℤ-graded algebra

MSC classification

Primary: 16S50: Endomorphism rings; matrix rings
Secondary: 16W20: Automorphisms and endomorphisms 16S32: Rings of differential operators 16W50: Graded rings and modules
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 6 - 12
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author V. V. B. was supported by Graduiertenkolleg “Experimentelle und konstruktive Algebra” of the German Research Foundation (DFG). Author V. L. was supported by Project II.6 of SFB-TRR 195 “Symbolic Tools in Mathematics and their Applications” of the DFG.

References

Adjamagbo, K. and van den Essen, A. R. P., A proof of the equivalence of the Dixmier, Jacobian and Poisson conjectures. Acta Math. Vietnam. 32(2007), no. 2–3, 205–214.Google Scholar
Bass, H., Connel, E. H., and Wright, D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse. Bull. Amer. Math. Soc. (NS) 7(1982), 287–330. https://doi.org/10.1090/S0273-0979-1982-15032-7Google Scholar
Bavula, V. V., Finite-dimensionality of $\text{Ext}^{n}$and $\text{Tor}_{n}$of simple modules over a class of algebras. Funct. Anal. Appl. 25(1991), no. 3, 229–230. https://doi.org/10.1007/BF01085496Google Scholar
Bavula, V. V., Dixmier’s problem 5 for the Weyl algebra. J. Algebra 283(2005), no. 2, 604–621. https://doi.org/10.1016/j.jalgebra.2004.09.013Google Scholar
Bavula, V. V., A question of Rentschler and the Dixmier problem. Ann. of Math. 154(2001), no. 3, 683–702. https://doi.org/10.2307/3062144Google Scholar
Bavula, V. V., The Jacobian conjecture implies the Dixmier problem. arxiv:0512250Google Scholar
Bavula, V. V., An analogue of the conjecture of Dixmier is true for the ring of polynomial integro-differential operators. J. Algebra 372(2012), 237–250. https://doi.org/10.1016/j.jalgebra.2012.09.009Google Scholar
Belov-Kanel, A. and Kontsevich, M., The Jacobian conjecture is stably equivalent to the Dixmier conjecture. Moscow Math. J. 7(2007), no. 2, 209–218. https://doi.org/10.17323/1609-4514-2007-7-2-209-218Google Scholar
Dixmier, J., Sur les algèbres de Weyl. Bull. Soc. Math. France 96(1968), 209–242.Google Scholar
Joseph, A., The Weyl algebra—semisimple and nilpotent elements. Amer. J. Math. 97(1975), no. 3, 597–615. https://doi.org/10.2307/2373768Google Scholar
Tsuchimoto, Y., Endomorphisms of Weyl algebra and p-curvatures. Osaka J. Math. 42(2005), no. 2, 435–452.Google Scholar