Published online by Cambridge University Press: 04 November 2019
With entries of the adjacency matrix of a simple graph being regarded as elements of 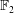 $\mathbb{F}_{2}$, it is proved that a finite commutative ring
$\mathbb{F}_{2}$, it is proved that a finite commutative ring 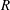 $R$ with
$R$ with 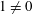 $1\neq 0$ is a Boolean ring if and only if either
$1\neq 0$ is a Boolean ring if and only if either 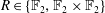 $R\in \{\mathbb{F}_{2},\mathbb{F}_{2}\times \mathbb{F}_{2}\}$ or the eigenvalues (in the algebraic closure of
$R\in \{\mathbb{F}_{2},\mathbb{F}_{2}\times \mathbb{F}_{2}\}$ or the eigenvalues (in the algebraic closure of 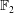 $\mathbb{F}_{2}$) corresponding to the zero-divisor graph of
$\mathbb{F}_{2}$) corresponding to the zero-divisor graph of 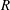 $R$ are precisely the elements of
$R$ are precisely the elements of 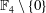 $\mathbb{F}_{4}\setminus \{0\}$ . This is achieved by observing a way in which algebraic behavior in a Boolean ring is encoded within Pascal’s triangle so that computations can be carried out by appealing to classical results from number theory.
$\mathbb{F}_{4}\setminus \{0\}$ . This is achieved by observing a way in which algebraic behavior in a Boolean ring is encoded within Pascal’s triangle so that computations can be carried out by appealing to classical results from number theory.