Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Moon, J. W.
1964.
Tournaments With a Given Automorphism Group.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
485.
Narayana, T.V.
and
Bent, D.H.
1964.
Computation of the Number of Score Sequences in Round-Robin Tournaments.
Canadian Mathematical Bulletin,
Vol. 7,
Issue. 1,
p.
133.
Wright, E. M.
1970.
The number of irreducible tournaments.
Glasgow Mathematical Journal,
Vol. 11,
Issue. 2,
p.
97.
Wyman, M.
1972.
Leo Moser 1921-1970.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 1,
p.
1.
1973.
Graphical Enumeration.
p.
253.
1975.
Abstract Analytic Number Theory.
Vol. 12,
Issue. ,
p.
297.
Blass, Andreas
and
Harary, Frank
1979.
Properties of almost all graphs and complexes.
Journal of Graph Theory,
Vol. 3,
Issue. 3,
p.
225.
Łuczak, Tomasz
Ruciński, Andrzej
and
Gruszka, Jacek
1996.
On the evolution of a random tournament.
Discrete Mathematics,
Vol. 148,
Issue. 1-3,
p.
311.
Pan, Linqiang
Zhou, Guofei
and
Zhang, Kemin
1999.
A note on hypertournaments.
Chinese Science Bulletin,
Vol. 44,
Issue. 16,
p.
1460.
Hanson, Denis
and
Moon, John W.
2004.
Weakening arcs in tournaments.
Journal of Graph Theory,
Vol. 45,
Issue. 2,
p.
142.
Rubinstein, Ariel
and
Segal, Uzi
2012.
On the likelihood of cyclic comparisons.
Journal of Economic Theory,
Vol. 147,
Issue. 6,
p.
2483.
Reid, K
2013.
Handbook of Graph Theory, Second Edition.
Vol. 20134658,
Issue. ,
p.
196.
Stockmeyer, Paul
2013.
Handbook of Graph Theory, Second Edition.
Vol. 20134658,
Issue. ,
p.
626.
Conrey, Brian
Gabbard, James
Grant, Katie
Liu, Andrew
and
Morrison, Kent E.
2016.
Intransitive Dice.
Mathematics Magazine,
Vol. 89,
Issue. 2,
p.
133.
KRIVELEVICH, MICHAEL
KWAN, MATTHEW
and
SUDAKOV, BENNY
2016.
Cycles and Matchings in Randomly Perturbed Digraphs and Hypergraphs.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 6,
p.
909.
Saile, Christian
and
Suksompong, Warut
2018.
Web and Internet Economics.
Vol. 11316,
Issue. ,
p.
393.
Saile, Christian
and
Suksompong, Warut
2020.
Robust bounds on choosing from large tournaments.
Social Choice and Welfare,
Vol. 54,
Issue. 1,
p.
87.
Tarbush, Bassel
2020.
Random Preferences, Acyclicity, and the Threshold of Rationality.
SSRN Electronic Journal ,
Archer, Kassie
Gessel, Ira M.
Graves, Christina
and
Liang, Xuming
2020.
Counting acyclic and strong digraphs by descents.
Discrete Mathematics,
Vol. 343,
Issue. 11,
p.
112041.
Monteil, Thierry
and
Nurligareev, Khaydar
2021.
Extended Abstracts EuroComb 2021.
Vol. 14,
Issue. ,
p.
823.
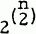 possible ones, will be irreducible. p(1)=1, by definition.
possible ones, will be irreducible. p(1)=1, by definition.