Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2025-01-01T08:56:56.407Z Has data issue: false hasContentIssue false
  • English
  • Français

An Inequality for Positive Semidefinite Hermitian Matrices(1)

Published online by Cambridge University Press:  20 November 2018

Russell Merris
Russell Merris*
Affiliation:
National Bureau of Standards, Washington, D.C. 20234California State University, Hayward, Ca 94542
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A and B be positive semidefinite Hermitian n-square matrices. If A—B is positive semidefinite, write A≥B. Haynsworth [1] has proved that if A≥B then det(A+B)≥det A+n det B.

Let G be a subgroup of the symmetric group, Sn, and let λ be a character on G. Let

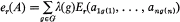
where A = (aij) and Er is the rth elementary symmetric function.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 1 , 01 March 1974 , pp. 131 - 132
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Haynsworth, Emilie V., Applications of an inequality for the Schur complement, Proc. Amer. Math. Soc. 24 (1970) 512-516.Google Scholar
2. Merris, Russell,A dominance theorem for partitioned hermitian matrices, Trans. Amer. Math. Soc. 164 (1972) 341-352.Google Scholar
3. Merris, Russell Inequalities for matrix functions, J. Algebra, 22 (1972) 451-460.Google Scholar