Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guiasu, Silviu
1990.
A classification of the main probability distributions by minimizing the weighted logarithmic measure of deviation.
Annals of the Institute of Statistical Mathematics,
Vol. 42,
Issue. 2,
p.
269.
Guariglia, Emanuel
2021.
Fractional calculus, zeta functions and Shannon entropy.
Open Mathematics,
Vol. 19,
Issue. 1,
p.
87.


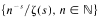 on the positive integers, for any
on the positive integers, for any 