Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T19:55:14.551Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Dimension of Proper CAT(0) Spaces that are Homeomorphic to the Plane

Published online by Cambridge University Press:  20 November 2018

Naotsugu Chinen  and
Tetsuya Hosaka
Naotsugu Chinen
Affiliation:
Hiroshima Institute of Technology, Hiroshima 731-5193, Japan
Tetsuya Hosaka
Affiliation:
Department of Mathematics, Faculty of Education, Utsunomiya University, Utsunomiya, 321-8505, Japan e-mail: naochin@cc.it-hiroshima.ac.jphosaka@cc.utsunomiya-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate a proper 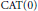$\text{CAT(0)}$ space 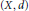$(X,\,d)$ that is homeomorphic to 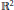${{\mathbb{R}}^{2}}$ and we show that the asymptotic dimension asdim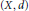$(X,\,d)$ is equal to 2.

Keywords

20F6954F4520F65asymptotic dimensionCAT(0) spaceplane
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 629 - 638
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature. Fundamental Principles of Mathematical Sciences, 319, Springer-Verlag, Berlin, 1999.Google Scholar
[2] Bell, G. and Dranishnikov, A. N., Asymptotic dimension. Topology Appl. 155(2008), no. 12, 1265–1296. doi:10.1016/j.topol.2008.02.011Google Scholar
[3] Davis, M. W., Nonpositive curvature and reflection groups. In: Handbook of geometric topology, North-Holland, Amsterdam, 2002, pp. 373–422.Google Scholar
[4] Davis, M. W., The cohomology of a Coxeter group with group ring coefficients. Duke Math. J. 91(1998), no. 2, 297–314. doi:10.1215/S0012-7094-98-09113-XGoogle Scholar
[5] Dranishnikov, A. N., Asymptotic topology. Uspekhi Mat. Nauk 55(2000), no. 6, 71–116; translation in Russian Math. Surveys 55(2000), no. 6, 1085–1129. doi:10.1070/rm2000v055n06ABEH000334Google Scholar
[6] Dranishnikov, A. N. and Januszkiewicz, T., Every Coxeter group acts amenably on a compact space. In: Proceedings of the 1999 Topology and Dynamics Conference (Salt Lake City, UT). Topology Proc. 24(1999), Spring, 135–141.Google Scholar
[7] Dranishnikov, A. N., Keesling, J., and Uspenskij, V. V., On the Higson corona of uniformly contractible spaces. Topology 37(1998), no. 4, 791–803. doi:10.1016/S0040-9383(97)00048-7Google Scholar
[8] Dranishnikov, A. N. and Schroeder, V., Embedding of hyperbolic Coxeter groups into products of binary trees and aperiodic tilings. http://arxiv.org/abs/math/0504566.Google Scholar
[9] Gromov, M., Asymptotic invariants for infinite groups. In: Geometric group theory, vol. 2, London Math. Soc. Lecture Note Ser., 182, Cambridge University Press, Cambridge, 1993, pp. 1–295.Google Scholar
[10] Hosaka, T., On the cohomology of Coxeter groups. J. Pure Appl. Algebra 162(2001), no. 2–3, 291–301. doi:10.1016/S0022-4049(00)00115-8Google Scholar
[11] Moussong, G., Hyperbolic Coxeter groups. Ph. D. thesis, Ohio State University, 1988.Google Scholar
[12] Roe, J., Hyperbolic groups have finite asymptotic dimension. Proc. Amer. Math. Soc. 133(2005), no. 9, 2489–2490. doi:10.1090/S0002-9939-05-08138-4Google Scholar
[13] Spanier, E. H., Algebraic topology. McGraw-Hill Book Co., New York-Toronto-London, 1966.Google Scholar
[14] Wilder, R. L., Topology of manifolds. American Mathematical Society Colloquium Publications, 32, American Mathematical Society, New York, NY, 1949.Google Scholar
[15] Yu, G., The Novikov conjecture for groups with finite asymptotic dimension. Ann. of Math. 147(1998), no. 2, 325–355. doi:10.2307/121011Google Scholar