Published online by Cambridge University Press: 20 November 2018
We study boundedness properties of the  $q$-mean-square operator
$q$-mean-square operator 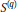 {{S}^{(q)}} on
{{S}^{(q)}} on 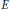 $E$-valued analytic martingales, where
$E$-valued analytic martingales, where 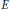 $E$ is a complex quasi-Banach space and
$E$ is a complex quasi-Banach space and 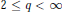 $2\,\le \,q\,<\,\infty $. We establish that a.s. finiteness of
$2\,\le \,q\,<\,\infty $. We establish that a.s. finiteness of 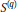 ${{S}^{(q)}}$ for every bounded
${{S}^{(q)}}$ for every bounded 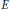 $E$-valued analytic martingale implies strong
$E$-valued analytic martingale implies strong 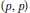 $(p,\,p)$-type estimates for
$(p,\,p)$-type estimates for 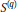 ${{S}^{(q)}}$ and all
${{S}^{(q)}}$ and all 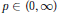 $p\,\in \,(0,\,\infty )$. Our results yield new characterizations (in terms of analytic and stochastic properties of the function
$p\,\in \,(0,\,\infty )$. Our results yield new characterizations (in terms of analytic and stochastic properties of the function 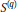 ${{S}^{(q)}}$) of the complex spaces
${{S}^{(q)}}$) of the complex spaces 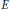 $E$ that admit an equivalent
$E$ that admit an equivalent  $q$-uniformly
$q$-uniformly 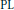 $\text{PL}$-convex quasi-norm. We also obtain a vector-valued extension (and a characterization) of part of an observation due to Bourgain and Davis concerning the
$\text{PL}$-convex quasi-norm. We also obtain a vector-valued extension (and a characterization) of part of an observation due to Bourgain and Davis concerning the 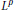 ${{L}^{p}}$-boundedness of the usual square-function on scalar-valued analytic martingales.
${{L}^{p}}$-boundedness of the usual square-function on scalar-valued analytic martingales.