Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T21:05:29.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds on Multiple Self-avoiding Polygons

Published online by Cambridge University Press:  20 November 2018

Kyungpyo Hong  and
Seungsang Oh
Kyungpyo Hong
Affiliation:
National Institute for Mathematical Sciences, Daejeon 34047, Korea, e-mail : kphong@nims.re.kr
Seungsang Oh
Affiliation:
Department of Mathematics, Korea University, Seoul 02841, Korea, e-mail : seungsang@korea.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A self-avoiding polygon is a lattice polygon consisting of a closed self-avoiding walk on a square lattice. Surprisingly little is known rigorously about the enumeration of self-avoiding polygons, although there are numerous conjectures that are believed to be true and strongly supported by numerical simulations. As an analogous problemto this study, we considermultiple self-avoiding polygons in a confined region as a model for multiple ring polymers in physics. We find rigorous lower and upper bounds for the number 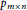${{p}_{m\times n}}$ of distinct multiple self-avoiding polygons in the 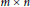$m\,\times \,n$ rectangular grid on the square lattice. For $m\,=\,2,\,{{p}_{2\times n}}\,=\,{{2}^{n-1}}\,-1$. And for integers 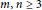$m,\,n\,\ge \,3$,

$${{2}^{m+n-3}}\left( \frac{17}{10} \right){{\,}^{\left( m-2 \right)\left( n-2 \right)}}\,\le \,{{p}_{m\times n}}\,\le \,{{2}^{m+n-3}}\left( \frac{31}{16} \right){{\,}^{\left( m-2 \right)\left( n-2 \right)}}.$$

Keywords

57M2582B2082B4182D60ring polymerself-avoiding polygon
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 518 - 530
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bousquet-Melou, M., Guttmann, A., and Jensen, I., Self-avoiding walks crossing a Square. J. Phys. A 38(2005), no. 42, 9159–9181. http://dx.doi.org/10.1088/0305-4470/38/42/001Google Scholar
[2] Flory, P., The configuration of real polymer chains. J. Chem. Phys. 17(1949), 303–310.Google Scholar
[3] Guttmann, A., ed., Polygons, polyominos, and polycubes. Lecture Notes in Physics, 775, Springer, Dordrecht, 2009. http://dx.doi.org/10.1007/978-1-4020-9927-4Google Scholar
[4] Hammersley, J. M., The number of polygons on a lattice. Proc. Cambridge Philos. Soc. 57(1961), 516–523.Google Scholar
[5] Hong, K., Lee, H., Lee, H. J., and Oh, S., Upper bound on the total number ofknot n-mosaics. J. Knot Theory Ramifications 23(2014), no. 13, 1450065. http://dx.doi.Org/10.1142/S0218216514500655Google Scholar
[6] Hong, K., Lee, H., Lee, H. J., and Oh, S., Small knot mosaics andpartition matrices. J. Phys. A 47(2014), no. 43, 435201. http://dx.doi.org/10.1088/1751-8113/47/43/435201Google Scholar
[7] van Rensburg, E. Janse, Thoughts on lattice knot statistics. J. Math. Chem. 45(2009), no. 1, 7–38. http://dx.doi.org/10.1007/s10910-008-9364-9Google Scholar
[8] Lee, H. J., Hong, K., Lee, H., and Oh, S., Mosaic number of knots. J. Knot Theory Ramifications 23(2014), no. 13, 1450069. http://dx.doi.org/10.1142/S0218216514500692Google Scholar
[9] Lomonaco, S. and Kauffman, L., Quantum knots and mosaics. Quantum Inf. Process. 7(2008), no. 2-3, 85–115. http://dx.doi.org/10.1007/s11128-008-0076-7Google Scholar
[10] Madras, N. and Slade, G., The Self-avoiding walk. Probability and its applications. Birkhäuser Boston, Boston, MA, 1993.Google Scholar
[11] Oh, S., Hong, K., Lee, H., and Lee, H. J., Quantum knots and the number ofknot mosaics. Quantum Inf. Process. 14(2015), no. 3, 801–811. http://dx.doi.org/10.1007/s11128-014-0895-7Google Scholar