Article contents
Closed Left Ideal Decompositions of U(G)
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 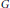 $G$ be an infinite discrete group and let
$G$ be an infinite discrete group and let 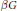 $\beta G$ be the Stone-Čech compactification of
$\beta G$ be the Stone-Čech compactification of 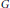 $G$. We take the points of
$G$. We take the points of 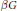 $\beta G$ to be the ultrafilters on
$\beta G$ to be the ultrafilters on 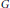 $G$, identifying the principal ultrafilters with the points of
$G$, identifying the principal ultrafilters with the points of 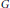 $G$. The set
$G$. The set 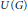 $U\left( G \right)$ of uniform ultrafilters on
$U\left( G \right)$ of uniform ultrafilters on 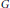 $G$ is a closed two-sided ideal of
$G$ is a closed two-sided ideal of 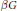 $\beta G$. For every
$\beta G$. For every 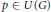 $p\,\in \,U\left( G \right)$, define
$p\,\in \,U\left( G \right)$, define 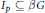 ${{I}_{p}}\,\subseteq \,\beta G$ by
${{I}_{p}}\,\subseteq \,\beta G$ by 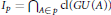 ${{I}_{p}}\,=\,{{\bigcap }_{A\in p}}\text{cl}\left( GU\left( A \right) \right)$, where
${{I}_{p}}\,=\,{{\bigcap }_{A\in p}}\text{cl}\left( GU\left( A \right) \right)$, where 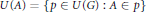 $U\left( A \right)\,=\,\left\{ p\,\in \,U\left( G \right)\,:\,A\in \,p \right\}$. We show that if
$U\left( A \right)\,=\,\left\{ p\,\in \,U\left( G \right)\,:\,A\in \,p \right\}$. We show that if 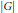 $\left| G \right|$ is a regular cardinal, then
$\left| G \right|$ is a regular cardinal, then 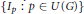 $\left\{ {{I}_{p}}\,:\,p\,\in \,U\left( G \right) \right\}$ is the finest decomposition of
$\left\{ {{I}_{p}}\,:\,p\,\in \,U\left( G \right) \right\}$ is the finest decomposition of 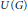 $U\left( G \right)$ into closed left ideals of
$U\left( G \right)$ into closed left ideals of 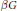 $\beta G$ such that the corresponding quotient space of
$\beta G$ such that the corresponding quotient space of 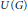 $U\left( G \right)$ is Hausdorff.
$U\left( G \right)$ is Hausdorff.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 6
- Cited by


