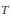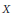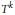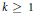Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chavan, Sameer
and
Trivedi, Shailesh
2016.
An analytic model for left-invertible weighted shifts on directed trees: Table 1..
Journal of the London Mathematical Society,
Vol. 94,
Issue. 1,
p.
253.