Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T18:14:28.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Connected Numbers and the Embedded Topology of Plane Curves

Published online by Cambridge University Press:  20 November 2018

Taketo Shirane
Taketo Shirane*
Affiliation:
National Institute of Technology, Ube College, Tokiwadai 2-14, Ube 755-8555, Japan, e-mail: tshirane@ube-k.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The splitting number of a plane irreducible curve for a Galois cover is effective in distinguishing the embedded topology of plane curves. In this paper, we define the connected number of a plane curve (possibly reducible) for a Galois cover, which is similar to the splitting number. By using the connected number, we distinguish the embedded topology of Artal arrangements of degree 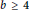$b\,\ge \,4$, where an Artal arrangement of degree $b$ is a plane curve consisting of one smooth curve of degree $b$ and three of its total inflectional tangents.

Keywords

14H3014H5014F45plane curvesplitting curveZariski paircyclic coversplitting number
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 650 - 658
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Artal-Bartolo, E., Sur les couples de Zariski. J. Algebraic Geom. 3 (1994), 223–247.Google Scholar
[2] Artal-Bartolo, E., Carmona, J., and Cogolludo-Agustin, J. I., Braid monodromy and topology of plane curves. Duke Math. J. 118 (2003), no. 2, 261–278. http://dx.doi.Org/10.1215/S0012-7094-03-11823-2Google Scholar
[3] Artal-Bartolo, E. and Tokunaga, H., Zariski k-plets of rational curve arrangements and dihedral Covers. Topology Appl. 142 (2004), 227–233. http://dx.doi.Org/10.1016/j.topol.2004.02.003Google Scholar
[4] Bannai, S., A note on Splitting curves of plane quartics and multi-sections of rational elliptic surfaces. Topology Appl. 202 (2016), 428–439. http://dx.doi.Org/10.1016/j.topol.2016.02.005Google Scholar
[5] Bannai, S., Guerville-Balle, B., Shirane, T., and Tokunaga, H., On the topology of arrangements of a cubic and its inflectional tangents. Proc. Japan Acad. Ser. A Math. Sei. 93 (2017), no. 6, 50–53. http://dx.doi.org/10.3792/pjaa.93.50Google Scholar
[6] Bannai, S. and Shirane, T., Nodal curves with a contact-conic and Zariskipairs. arxiv:1608.03760Google Scholar
[7] Coppens, M. and Kato, T., Non-trivial linear Systems on smooth plane curves. Math. Nachr. 166(1994) 71–82. http://dx.doi.Org/10.1002/mana.19941660106Google Scholar
[8] Degtyarev, A., On deformations of Singular plane sextics. J. Algebraic Geom. 17 (2008), no. 1, 101–135. http://dx.doi.Org/10.1090/S1056-3911-07-00469-9Google Scholar
[9] Guerville-Balle, B. and Meilhan, J. B., A linking invariant for algebraic curves. arxiv:1602.04916Google Scholar
[10] Guerville-Balle, B. and Shirane, T., Non-homotopicity ofthe linking set of algebraic plane curves. J. Knot Theory Ramifications, to appear.Google Scholar
[11] Oka, M., A new Alexander-equivalent Zariski pair. Acta Math. Vietnam 27 (2002), 349–357.Google Scholar
[12] Pardini, R., Abelian Covers of algebraic varieties. J. Reine Angew. Math. 417 (1991), 191–213. http://dx.doi.Org/10.1515/crlU991.417.191Google Scholar
[13] Shimada, I., Equisingular families of plane curves with many connected components. Vietnam J. Math. 31 (2003), no. 2, 193–205.Google Scholar
[14] Shirane, T., A note on Splitting numbers for Galois Covers and n\-equivalent Zariski k-plets. Proc. Amer. Math. Soc. 145 (2017), no. 3, 1009–1017. http://dx.doi.Org/10.1090/proc/13298Google Scholar
[15] Tokunaga, H., A remark on E. Artal-Bartolo's paper: “On Zariski pairs” J. Algebraic Geom. 3 (1994), no. 2, 223–247; MR1257321 (94m:14033)]. Kodai Math. J. 19 (1996), no. 2, 207–217.Google Scholar
[16] Tokunaga, H., Dihedral coverings of algebraic surfaces and their application. Trans. Amer. Math. Soc. 352 (2000), 4007–4017. http://dx.doi.org/10.1090/S0002-9947-00-02524-1Google Scholar
[17] Zariski, O., On the problem of existence of algebraic funetions oftwo variables possessing a given branch curve. Amer. J. Math. 51 (1929), 305–328. http://dx.doi.Org/10.2307/2370712Google Scholar