Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bartolo, Rossella
Caponio, Erasmo
Germinario, Anna Valeria
and
Sánchez, Miguel
2011.
Convex domains of Finsler and Riemannian manifolds.
Calculus of Variations and Partial Differential Equations,
Vol. 40,
Issue. 3-4,
p.
335.
Cooper, Daryl
Long, Darren
and
Tillmann, Stephan
2018.
Deforming convex projective manifolds.
Geometry & Topology,
Vol. 22,
Issue. 3,
p.
1349.


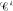 convex functions cannot be approximated by
convex functions cannot be approximated by 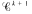 convex functions (
convex functions (