Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T14:55:50.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of topological Azumaya algebras

Part of: Homotopy groups Homotopy theory Operations and obstructions

Published online by Cambridge University Press:  29 June 2021

Niny Arcila-Maya
Niny Arcila-Maya*
Affiliation:
Department of Mathematics, The University of British Columbia, Room 121, 1984 Mathematics Road, Vancouver, BCV6T 1Z2, Canada
*
ninyam@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 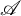$\mathscr {A}$ be a topological Azumaya algebra of degree 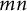$mn$ over a CW complex X. We give conditions for the positive integers m and n, and the space X so that 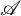$\mathscr {A}$ can be decomposed as the tensor product of topological Azumaya algebras of degrees m and n. Then we prove that if 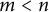$m<n$ and the dimension of X is higher than 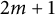$2m+1$ , 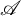$\mathscr {A}$ may not have such decomposition.

Keywords

Topological Azumaya algebraprojective unitary group

MSC classification

Primary: 55P99: None of the above, but in this section
Secondary: 55Q52: Homotopy groups of special spaces 55S45: Postnikov systems, $k$-invariants 16H05: Separable algebras (e.g., quaternion algebras, Azumaya algebras, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 2 , June 2022 , pp. 506 - 524
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antieau, B. and Williams, B., The topological period-index problem over 6-complexes. J. Topol. 7(2013), no. 3, 617–640. http://doi.org/10.1112/jtopol/jtt042 CrossRefGoogle Scholar
Antieau, B. and Williams, B., Unramified division algebras do not always contain Azumaya maximal orders. Invent. Math. 197(2014), no. 1, 47–56. http://doi.org/10.1007/s00222-013-0479-7 CrossRefGoogle Scholar
Antieau, B. and Williams, B., The period-index problem for twisted topological K-theory. Geom. Topol. 18(2014), no. 2, 1115–1148. http://doi.org/10.2140/gt.2014.18.1115 CrossRefGoogle Scholar
Auslander, M. and Goldman, O., The Brauer group of a commutative ring. Trans. Amer. Math. Soc. 97(1960), no. 3, 367–409. http://doi.org/10.1090/S0002-9947-1960-0121392-6 CrossRefGoogle Scholar
Azumaya, G., On maximally central algebras. Nagoya Math. J. 2(1951), 119–150. http://doi.org/10.1017/S0027763000010114 CrossRefGoogle Scholar
Bott, R., The space of loops on a Lie group. Michigan Math. J. 5(1958), no. 1, 35–61. http://doi.org/10.1307/mmj/1028998010 CrossRefGoogle Scholar
Grothendieck, A., Le groupe de Brauer: I. Algèbres d’Azumaya et interprétations diverses . In: Séminaire Bourbaki: années 1964/65 1965/66, exposés 277-312, Séminaire Bourbaki, 9, Société mathématique de France, 1966, pp. 199–219. talk:290.Google Scholar
Hatcher, A., Algebraic topology. Cambridge University Press, Cambridge, 2002.Google Scholar
Mimura, M., Chapter 19—Homotopy theory of Lie groups. In: James, I. (ed.), Handbook of algebraic topology. North-Holland, Amsterdam, 1995, pp. 951–991. http://doi.org/10.1016/B978-044481779-2/50020-1 CrossRefGoogle Scholar
Saltman, D. J., Lectures on division algebras. CBMS Reg. Conf. Ser. Math., 94, AMS, Providence, RI, 1999; on behalf of CBMS, Washington, DC. http://doi.org/10.1090/cbms/094 CrossRefGoogle Scholar
Spanier, E. H., Algebraic topology. Springer, New York, NY, 1981. http://doi.org/10.1007/978-1-4684-9322-1 CrossRefGoogle Scholar
Steenrod, N., The topology of fibre bundles (PMS-14). Princeton University Press, Princeton, NJ, 1951. http://doi.org/10.1515/9781400883875 CrossRefGoogle Scholar