Article contents
Determining sets for holomorphic functions on the symmetrized bidisk
Published online by Cambridge University Press: 31 January 2023
Abstract
A subset 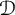 ${\mathcal D}$ of a domain
${\mathcal D}$ of a domain 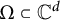 $\Omega \subset {\mathbb C}^d$ is determining for an analytic function
$\Omega \subset {\mathbb C}^d$ is determining for an analytic function 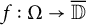 $f:\Omega \to \overline {{\mathbb D}}$ if whenever an analytic function
$f:\Omega \to \overline {{\mathbb D}}$ if whenever an analytic function 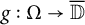 $g:\Omega \rightarrow \overline {{\mathbb D}}$ coincides with f on
$g:\Omega \rightarrow \overline {{\mathbb D}}$ coincides with f on 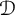 ${\mathcal D}$, equals to f on whole
${\mathcal D}$, equals to f on whole  $\Omega $. This note finds several sufficient conditions for a subset of the symmetrized bidisk to be determining. For any
$\Omega $. This note finds several sufficient conditions for a subset of the symmetrized bidisk to be determining. For any 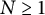 $N\geq 1$, a set consisting of
$N\geq 1$, a set consisting of 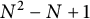 $N^2-N+1$ many points is constructed which is determining for any rational inner function with a degree constraint. We also investigate when the intersection of the symmetrized bidisk intersected with some special algebraic varieties can be determining for rational inner functions.
$N^2-N+1$ many points is constructed which is determining for any rational inner function with a degree constraint. We also investigate when the intersection of the symmetrized bidisk intersected with some special algebraic varieties can be determining for rational inner functions.
Keywords
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
B.K.D. is supported by the Mathematical Research Impact Centric Support (MATRICS) grant, File No: MTR/2021/000560, by the Science and Engineering Research Board (SERB), Department of Science & Technology (DST), Government of India. P.K. is supported by the University Grants Commission Centre for Advanced Studies. The research works of H.S. is supported by DST-INSPIRE Faculty Fellowship DST/INSPIRE/04/2018/002458.
References
- 3
- Cited by


