Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T06:01:27.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Dihedral Groups of Order 2p of Automorphisms of Compact Riemann Surfaces of Genus p – 1

Published online by Cambridge University Press:  20 November 2018

Qingjie Yang  and
Weiting Zhong
Qingjie Yang
Affiliation:
Department of Mathematics, Renmin University of China, Beijing, China, 100872. e-mail: yangqj@ruc.edu.cn, e-mail: zhwt 2007@yahoo.com.cn
Weiting Zhong
Affiliation:
Department of Mathematics, Renmin University of China, Beijing, China, 100872. e-mail: yangqj@ruc.edu.cn, e-mail: zhwt 2007@yahoo.com.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove that there is only one conjugacy class of dihedral group of order 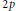$2p$ in the 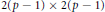$2\left( p\,-\,1 \right)\,\times \,2\left( p\,-\,1 \right)$ integral symplectic group that can be realized by an analytic automorphism group of compact connected Riemann surfaces of genus 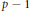$p\,-\,1$. A pair of representative generators of the realizable class is also given.

Keywords

20H2557M60dihedral groupautomorphism groupRiemann surfaceintegral symplectic matrixfundamental domain
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 196 - 206
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Breuer, T., Characters and automorphism groups of compact Riemann surfaces. London Mathematical Society Lecture Note Series, 280, Cambridge University Press, Cambridge, 2000.Google Scholar
[2] Eckmann, B. and Müller, H., Plane motion groups and virtual Poincaré duality of dimension two. Invent. Math. 69 (1982), no. 2, 293–310. http://dx.doi.org/10.1007/BF01399508 Google Scholar
[3] Farkas, H. M. and Kra, I., Riemann surfaces. Second ed., Graduate Texts in Mathematics, 71, Springer-Verlag, New York, 1992.Google Scholar
[4] Gabai, D., Convergence groups are Fuchsian groups. Ann. of Math. 136 (1992), no. 3, 447–510. http://dx.doi.org/10.2307/2946597 Google Scholar
[5] George Michael, A. A., Metacyclic groups of automorphisms of compact Riemann surfaces. Hiroshima Math. J. 31 (2001), no. 1, 117–132. Google Scholar
[6] Harvey, W. J., Spaces of discrete groups. In: Discrete groups and automorphic functions (Proc. Conf. Cambridge, 1975), Academic Press, London, 1977, pp. 295–348..Google Scholar
[7] Jones, G. and Singerman, D., Complex functions. An algebraic and geometric viewpoint. Cambridge University Press, Cambridge, 1987.Google Scholar
[8] Kerckhoff, S. P., The Nielsen realization problem. Ann. of Math. 117 (1983), no. 2, 235–265. http://dx.doi.org/10.2307/2007076 Google Scholar
[9] Massey, W. S., Singular homology theory. Graduate Texts in Mathematics, 70, Spring-Verlag, New York-Berlin, 1980.Google Scholar
[10] Nielsen, J., Abbildungklassen Endliche Ordung. Acta Math. 75 (1943), 23–115. http://dx.doi.org/10.1007/BF02404101 Google Scholar
[11] Sjerve, D. and Yang, Q., Conjugacy classes of p-torsion in SPp-1(ℤ). J. Algebra 195 (1997), no. 2, 580–603. http://dx.doi.org/10.1006/jabr.1997.7084 Google Scholar
[12] Yang, Q., Dihedral groups of automorphisms of compact Riemann surfaces. Canad. Math. Bull. 41 (1998), no. 2, 252–256. http://dx.doi.org/10.4153/CMB-1998-036-7 Google Scholar
[13] Yang, Q., Matrix classes realized by automorphisms of compact Riemann surfaces of genus two. Comm. Algebra 40 (2012), no. 7, 2343–2357. http://dx.doi.org/10.1080/00927872.2011.565491 Google Scholar