No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
A domain 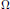 $\Omega $ is called a domain of injective holomorphy if there exists an injective holomorphic function
$\Omega $ is called a domain of injective holomorphy if there exists an injective holomorphic function 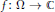 $f\,:\,\Omega \,\to \,\mathbb{C}$ that is non-extendable. We give examples of domains that are domains of injective holomorphy and others that are not. In particular, every regular domain
$f\,:\,\Omega \,\to \,\mathbb{C}$ that is non-extendable. We give examples of domains that are domains of injective holomorphy and others that are not. In particular, every regular domain 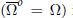 $(\overset{\multimap }{\mathop{\Omega }}\,\,=\,\Omega )$ is a domain of injective holomorphy, and every simply connected domain is a domain of injective holomorphy as well.
$(\overset{\multimap }{\mathop{\Omega }}\,\,=\,\Omega )$ is a domain of injective holomorphy, and every simply connected domain is a domain of injective holomorphy as well.