Published online by Cambridge University Press: 20 November 2018
A function f(x) is said to be completely monotonic on (0, ∞) if
1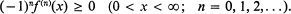
Familiar examples of such functions are given by f(x) = exp(—αx) and f(x) = (x+β)-α, where α ≥ 0, β ≥ 0. A discussion of completely monotonic functions is given in [5, Ch. IV].
This is a revised version of a note written while the author attended the Summer Research Institute of the Canadian Mathematical Congress, Université de Montréal, 1969. The writer is indebted to Professor Lee Lorch for some helpful comments.