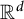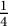1 Introduction
The main purpose of this paper is to construct explicit exponential bases on finite or infinite unions of intervals of the real line. We assume that our intervals have total measure one, until otherwise specified.
We recall that an exponential basis on a domain
![]() $D\subset \mathbb {R}^d$
is an unconditional Schäuder basis for
$D\subset \mathbb {R}^d$
is an unconditional Schäuder basis for
![]() $L^2(D)$
in the form of
$L^2(D)$
in the form of
![]() $\{e^{2\pi i \lambda _n \cdot x}\}_{n\in \mathbb {Z}^d }$
with
$\{e^{2\pi i \lambda _n \cdot x}\}_{n\in \mathbb {Z}^d }$
with
![]() $\lambda _n \in \mathbb {R}^d$
. An important example of exponential basis is the Fourier basis
$\lambda _n \in \mathbb {R}^d$
. An important example of exponential basis is the Fourier basis
![]() $ {\mathcal E}=\{e^{2\pi i n x}\}_{n\in \mathbb {Z} }$
for
$ {\mathcal E}=\{e^{2\pi i n x}\}_{n\in \mathbb {Z} }$
for
![]() $L^2(0,1)$
.
$L^2(0,1)$
.
Non-orthonormal exponential bases on intervals of the real line are well studied and well understood in the context of nonharmonic Fourier series (see [Reference Landau13, Reference Lev14, Reference Pavlov18, Reference Seip20] just to cite a few). Proving the existence of an exponential basis is in general a difficult problem, and constructing explicit bases can be even more difficult.
In [Reference Lev14], the author proved the existence of bases on finite unions of intervals under some conditions on the lengths of the intervals. It is proved in [Reference Kozma and Nitzan11] that exponential bases on any finite union of intervals exist, but the construction of such bases is not explicit. It is not clear whether exponential bases on arbitrary infinite unions of intervals exist or not.
In [Reference De Carli4], the author proves necessary and sufficient conditions for which sets in the form of
![]() $\{e^{2\pi i (n+\delta _{ j})x}\}_{n\in \mathbb {Z},{j\leq N}}$
are exponential bases on unions of N intervals of a unit length separated by integer gaps and gave an explicit expression for the frame constants of these bases. Such a result can be used to construct explicit exponential bases on intervals with rational endpoints. However, the conditions involve evaluating the eigenvalues of
$\{e^{2\pi i (n+\delta _{ j})x}\}_{n\in \mathbb {Z},{j\leq N}}$
are exponential bases on unions of N intervals of a unit length separated by integer gaps and gave an explicit expression for the frame constants of these bases. Such a result can be used to construct explicit exponential bases on intervals with rational endpoints. However, the conditions involve evaluating the eigenvalues of
![]() $N\times N$
matrices, which can be a difficult task. Some of the results in [Reference De Carli4] appear also in other papers, for example, in [Reference Kolountzakis10].
$N\times N$
matrices, which can be a difficult task. Some of the results in [Reference De Carli4] appear also in other papers, for example, in [Reference Kolountzakis10].
In [Reference Laba12], it is proved that if D is the union of two disjoint intervals of total length 1, then D has an orthonormal basis of exponentials if and only if it tiles
![]() $\mathbb {R}$
by translations. Recall that a measurable set
$\mathbb {R}$
by translations. Recall that a measurable set
![]() $D $
tiles
$D $
tiles
![]() $\mathbb {R}^d$
by translation if we can fill the space with translated copies of D without overlaps. Results for unions of three intervals that tile the real line are in [Reference Bose, Kumar, Krishnan and Madan3].
$\mathbb {R}^d$
by translation if we can fill the space with translated copies of D without overlaps. Results for unions of three intervals that tile the real line are in [Reference Bose, Kumar, Krishnan and Madan3].
In many applications, such as aircraft instrument communications, air traffic control simulation, or telemetry [Reference Fogel7], one can consider the possibility of obtaining sampling expansion which involved sample values of a function and its derivatives. That translated into finding bases of the form of
![]() $\{x^k e^{2\pi i x\lambda _n}\}_{n\in \mathbb {Z}}$
, with
$\{x^k e^{2\pi i x\lambda _n}\}_{n\in \mathbb {Z}}$
, with
![]() $k \in \mathbb {N}\cup \{0\}$
. See [Reference Selvan and Ghosh21].
$k \in \mathbb {N}\cup \{0\}$
. See [Reference Selvan and Ghosh21].
It is worth mentioning the recent [Reference Pfander, Shauna and Walnut19], where the authors partition the interval
![]() $[0,1]$
into intervals
$[0,1]$
into intervals
![]() $I_1$
, …,
$I_1$
, …,
![]() $I_n$
and the set
$I_n$
and the set
![]() $\mathbb {Z}$
into
$\mathbb {Z}$
into
![]() $\Lambda _1$
, …,
$\Lambda _1$
, …,
![]() $\Lambda _n$
such that the complex exponential functions with frequencies in
$\Lambda _n$
such that the complex exponential functions with frequencies in
![]() $\Lambda _k$
form a Riesz basis for
$\Lambda _k$
form a Riesz basis for
![]() $L^2(I_k)$
.
$L^2(I_k)$
.
The existence of orthonormal bases on a domain of
![]() $\mathbb {R}^d$
is a difficult problem related to the tiling properties of the domain. It has been recently proved in [Reference Lev and Matolcsi15] that convex sets tile
$\mathbb {R}^d$
is a difficult problem related to the tiling properties of the domain. It has been recently proved in [Reference Lev and Matolcsi15] that convex sets tile
![]() $\mathbb {R}^d$
by translations if and only if they have an exponential basis. In [Reference De Carli, Mizrahi and Tepper6], it is proved that the set
$\mathbb {R}^d$
by translations if and only if they have an exponential basis. In [Reference De Carli, Mizrahi and Tepper6], it is proved that the set
![]() ${\mathcal E} =\{e^{2\pi i n\cdot x}\}_{n\in \mathbb {Z}^d}$
is an exponential basis on a domain
${\mathcal E} =\{e^{2\pi i n\cdot x}\}_{n\in \mathbb {Z}^d}$
is an exponential basis on a domain
![]() $D\subset \mathbb {R}^d$
of measure
$D\subset \mathbb {R}^d$
of measure
![]() $1$
if and only if D tiles
$1$
if and only if D tiles
![]() $\mathbb {R}^d$
. Furthermore,
$\mathbb {R}^d$
. Furthermore,
![]() ${\mathcal E}$
is orthonormal for
${\mathcal E}$
is orthonormal for
![]() $L^2(D)$
.
$L^2(D)$
.
The aforementioned results in [Reference De Carli, Mizrahi and Tepper6] are related to Theorem 1 in [Reference Iosevich and Kolountzakis9], where it is proved that if a set
![]() $\{e^{2\pi i x \lambda }\}_{\lambda \in \Lambda }$
is an orthonormal basis on a domain
$\{e^{2\pi i x \lambda }\}_{\lambda \in \Lambda }$
is an orthonormal basis on a domain
![]() $D\subset \mathbb {R}$
, then
$D\subset \mathbb {R}$
, then
![]() $\Lambda $
is periodic, i.e.,
$\Lambda $
is periodic, i.e.,
![]() $\Lambda = T+\Lambda $
for some
$\Lambda = T+\Lambda $
for some
![]() $T\in \mathbb {N}$
.
$T\in \mathbb {N}$
.
1.1 Our results
Before we introduce our results, we need some more notations. By
![]() $m\in \mathbb {N}\cup \{\infty \}$
, we mean that m is either a natural number or it is infinity. We let
$m\in \mathbb {N}\cup \{\infty \}$
, we mean that m is either a natural number or it is infinity. We let
![]() $I=[0,1)$
. Given
$I=[0,1)$
. Given
![]() $0=a_0<a_1<\cdots <a_{m-1}<\cdots <1$
be a sequence for
$0=a_0<a_1<\cdots <a_{m-1}<\cdots <1$
be a sequence for
![]() $m\in \mathbb {N}\cup \{\infty \}$
, we let
$m\in \mathbb {N}\cup \{\infty \}$
, we let
![]() $I_j=[a_j, a_{j+1})$
, so that
$I_j=[a_j, a_{j+1})$
, so that
![]() $I= \bigcup I_j.$
$I= \bigcup I_j.$
Given
![]() $0=b_0<b_1<\cdots <b_{m-1}<\cdots $
, we let
$0=b_0<b_1<\cdots <b_{m-1}<\cdots $
, we let
We can also write
 $$ \begin{align} J=\bigcup_j [c_j-\gamma_j, c_j+\gamma_j) \quad\mbox{with }\ c_j=\frac{a_{j-1}+a_j}2+ b_j, \quad \gamma_j= \frac{a_j-a_{j-1}} 2. \end{align} $$
$$ \begin{align} J=\bigcup_j [c_j-\gamma_j, c_j+\gamma_j) \quad\mbox{with }\ c_j=\frac{a_{j-1}+a_j}2+ b_j, \quad \gamma_j= \frac{a_j-a_{j-1}} 2. \end{align} $$
Note that
![]() $\sum _j \gamma _j=1$
. So, on graph, we have
$\sum _j \gamma _j=1$
. So, on graph, we have

Let
![]() $\{x\}$
be the decimal part of a real number
$\{x\}$
be the decimal part of a real number
![]() $x,$
let
$x,$
let
![]() $\lfloor x\rfloor $
(the floor function) be the largest integer, that is,
$\lfloor x\rfloor $
(the floor function) be the largest integer, that is,
![]() $\leq x$
, and let
$\leq x$
, and let
![]() $\lceil x\rceil $
(the ceiling function) be the smallest integer, that is,
$\lceil x\rceil $
(the ceiling function) be the smallest integer, that is,
![]() $\geq x$
. If
$\geq x$
. If
![]() $E\subset \mathbb {R}$
, we define the distance function for
$E\subset \mathbb {R}$
, we define the distance function for
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $E\subset \mathbb {R}$
as
$E\subset \mathbb {R}$
as
![]() $\operatorname {dist}(E,x):=\min _{y\in E}\{ |y-x|\}$
or
$\operatorname {dist}(E,x):=\min _{y\in E}\{ |y-x|\}$
or
![]() $\operatorname {dist}(E,F):=\min _{y\in E, x\in F}\{ |y-x|\}.$
$\operatorname {dist}(E,F):=\min _{y\in E, x\in F}\{ |y-x|\}.$
Next, we introduce the sequence
![]() $\delta _n^*.$
Let
$\delta _n^*.$
Let
![]() $\beta>0$
be fixed; for every
$\beta>0$
be fixed; for every
![]() $n\in \mathbb {Z}$
, we let
$n\in \mathbb {Z}$
, we let
 $$ \begin{align} \delta_n^*=\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12.\\ \end{cases} \end{align} $$
$$ \begin{align} \delta_n^*=\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12.\\ \end{cases} \end{align} $$
We can see at once that
 $$ \begin{align*}\delta_n^*= \frac{\xi_n}{\beta} \min\left\{\{\beta n\},1-\{\beta n\}\right\}=\frac{\xi_n}{\beta}\operatorname{dist}{(\mathbb{Z},\beta n)}, \end{align*} $$
$$ \begin{align*}\delta_n^*= \frac{\xi_n}{\beta} \min\left\{\{\beta n\},1-\{\beta n\}\right\}=\frac{\xi_n}{\beta}\operatorname{dist}{(\mathbb{Z},\beta n)}, \end{align*} $$
where
 $$ \begin{align*} \xi_n = \begin{cases} 1, & \text{if } \{\beta n\} \geq \frac12, \\ -1, & \text{if } \{\beta n\} < \frac12. \\ \end{cases} \end{align*} $$
$$ \begin{align*} \xi_n = \begin{cases} 1, & \text{if } \{\beta n\} \geq \frac12, \\ -1, & \text{if } \{\beta n\} < \frac12. \\ \end{cases} \end{align*} $$
Let
where the
![]() $\delta _n^*$
are defined as in (1.3). Our main results are the following.
$\delta _n^*$
are defined as in (1.3). Our main results are the following.
Theorem 1.1 Let J be as in (1.1). If there exists
![]() $\beta \geq 1$
such that
$\beta \geq 1$
such that
![]() $\frac {b_k}{\beta }\in \mathbb {Z} $
for all k, then the set
$\frac {b_k}{\beta }\in \mathbb {Z} $
for all k, then the set
![]() ${\mathcal {B}}^*$
defined in (1.4) is an exponential basis for
${\mathcal {B}}^*$
defined in (1.4) is an exponential basis for
![]() $L^2(J).$
$L^2(J).$
Theorem 1.2 Let J and
![]() $\beta $
be as in Theorem 1.1. Let
$\beta $
be as in Theorem 1.1. Let
![]() $m\in \mathbb {N}$
, and let
$m\in \mathbb {N}$
, and let
![]() $\Lambda = \left \{n+\delta ^*_n\right \},$
where
$\Lambda = \left \{n+\delta ^*_n\right \},$
where
![]() $\delta ^*$
is as in (1.3). If
$\delta ^*$
is as in (1.3). If
![]() $\frac {b_k}{\beta }\in \mathbb {Z} $
for all
$\frac {b_k}{\beta }\in \mathbb {Z} $
for all
![]() $k=1,\ldots ,m-1$
, then the set
$k=1,\ldots ,m-1$
, then the set
![]() ${\mathcal E}(\frac {1}{\Delta }\mathbb {Z}\backslash \Lambda )$
is an exponential basis for
${\mathcal E}(\frac {1}{\Delta }\mathbb {Z}\backslash \Lambda )$
is an exponential basis for
![]() $L^2([0,\Delta ]\backslash J),$
where
$L^2([0,\Delta ]\backslash J),$
where
 $$ \begin{align*}\Delta=\left\lceil\frac{1+b_{m-1}}{\beta} \right\rceil \beta. \end{align*} $$
$$ \begin{align*}\Delta=\left\lceil\frac{1+b_{m-1}}{\beta} \right\rceil \beta. \end{align*} $$
We will prove in Lemma 3.1 that
![]() ${\mathcal {B}}^*$
is also a basis in
${\mathcal {B}}^*$
is also a basis in
![]() $L^2(0,1);$
our proof of Theorem 1.1 shows that
$L^2(0,1);$
our proof of Theorem 1.1 shows that
![]() ${\mathcal {B}}^*$
has the same frame constants in
${\mathcal {B}}^*$
has the same frame constants in
![]() $L^2(J)$
and
$L^2(J)$
and
![]() $L^2(0,1).$
$L^2(0,1).$
In our Theorem 1.1, the gaps
![]() $ b_k$
are integer multiples of
$ b_k$
are integer multiples of
![]() $\beta $
and so the set J is unbounded when
$\beta $
and so the set J is unbounded when
![]() $m=\infty $
. To the best of our knowledge, there are very few examples of exponential bases on unbounded sets in the literature. The existence of exponential frames on unbounded sets of finite measure has been recently proved in [Reference Nitzan, Olevskii and Ulanovskii16].
$m=\infty $
. To the best of our knowledge, there are very few examples of exponential bases on unbounded sets in the literature. The existence of exponential frames on unbounded sets of finite measure has been recently proved in [Reference Nitzan, Olevskii and Ulanovskii16].
We also observe that in Theorem 1.2, we cannot consider
![]() $m=\infty $
because J is unbounded, and in the proof, we need to consider a finite interval
$m=\infty $
because J is unbounded, and in the proof, we need to consider a finite interval
![]() $[0,\Delta ]$
that contains J.
$[0,\Delta ]$
that contains J.
Our paper is organized as follows: in Section 2, we recall some preliminaries and we prove some important lemmas. In Section 3, we prove our main results. In Section 4, we prove the result for unions of cubes in
![]() $\mathbb {R}^d$
and a stability result.
$\mathbb {R}^d$
and a stability result.
2 Preliminaries
We have used the excellent textbooks [Reference Heil8, Reference Young24] for the definitions and some of the results presented in this section.
Let H be a separable Hilbert space with inner product
![]() $\langle \,\, ,\, \rangle $
and norm
$\langle \,\, ,\, \rangle $
and norm
![]() $||\ ||=\sqrt {\langle \,\, , \, \rangle } $
. We will mostly work with
$||\ ||=\sqrt {\langle \,\, , \, \rangle } $
. We will mostly work with
![]() $L^2(D),$
where
$L^2(D),$
where
![]() $D\subset \mathbb {R}^d.$
So, the norm will be
$D\subset \mathbb {R}^d.$
So, the norm will be
![]() $||f||_2^2=\int _D |f(x)|^2 dx.$
We denote the characteristic function on D by
$||f||_2^2=\int _D |f(x)|^2 dx.$
We denote the characteristic function on D by
![]() $\chi _D.$
$\chi _D.$
A sequence of vectors
![]() ${\mathcal V}= \{v_j\}_{j\in \mathbb {Z} }$
in H is a Riesz basis if there exist constants
${\mathcal V}= \{v_j\}_{j\in \mathbb {Z} }$
in H is a Riesz basis if there exist constants
![]() $A, \ B>0$
such that, for any
$A, \ B>0$
such that, for any
![]() $w\in H$
and for all finite sequences
$w\in H$
and for all finite sequences
![]() $ \{a_j\}_{j\in J}\subset \mathbb {C} $
, the following inequalities hold:
$ \{a_j\}_{j\in J}\subset \mathbb {C} $
, the following inequalities hold:
 $$ \begin{align} A \sum_{j\in J} |a_j|^2 \leq &\Big\Vert \sum_{j\in J} a_j v_j \Big\Vert^2 \leq B \sum_{j\in J} |a_j|^2, \end{align} $$
$$ \begin{align} A \sum_{j\in J} |a_j|^2 \leq &\Big\Vert \sum_{j\in J} a_j v_j \Big\Vert^2 \leq B \sum_{j\in J} |a_j|^2, \end{align} $$
 $$ \begin{align} A||w||^2\leq &\sum_{j=1}^{\infty} |\langle w, v_j\rangle |^2\leq B ||w||^2. \end{align} $$
$$ \begin{align} A||w||^2\leq &\sum_{j=1}^{\infty} |\langle w, v_j\rangle |^2\leq B ||w||^2. \end{align} $$
The constants A and B are called frame constants of the basis. The left inequality in (2.1) implies that
![]() ${\mathcal V}$
is linearly independent, and the left inequality in (2.2) implies that
${\mathcal V}$
is linearly independent, and the left inequality in (2.2) implies that
![]() ${\mathcal V}$
is complete. If the condition (2.1) holds, we call
${\mathcal V}$
is complete. If the condition (2.1) holds, we call
![]() ${\mathcal V}$
a Riesz sequence. We call
${\mathcal V}$
a Riesz sequence. We call
![]() ${\mathcal V}$
a frame if the condition (2.2) holds. If the condition (2.2) holds and
${\mathcal V}$
a frame if the condition (2.2) holds. If the condition (2.2) holds and
![]() $A=B$
, then we call
$A=B$
, then we call
![]() ${\mathcal V}$
a tight frame. If
${\mathcal V}$
a tight frame. If
![]() $A=B=1,$
then we have a Parseval frame. The following lemma is well known, but for the reader’s convenience, we will prove it.
$A=B=1,$
then we have a Parseval frame. The following lemma is well known, but for the reader’s convenience, we will prove it.
Lemma 2.1 If a sequence of vectors
![]() ${\mathcal V}= \{v_j\}_{j\in \mathbb {Z} }$
is a frame with upper constant B, then the right inequality in (2.1) holds, i.e., for all finite sequences
${\mathcal V}= \{v_j\}_{j\in \mathbb {Z} }$
is a frame with upper constant B, then the right inequality in (2.1) holds, i.e., for all finite sequences
![]() $ \{a_j\}_{j\in J}\subset \mathbb {C}, $
$ \{a_j\}_{j\in J}\subset \mathbb {C}, $
 $$ \begin{align*}\Big\Vert \sum_{j\in J} a_j v_j \Big\Vert^2 \leq B \sum_{j\in J} |a_j|^2. \end{align*} $$
$$ \begin{align*}\Big\Vert \sum_{j\in J} a_j v_j \Big\Vert^2 \leq B \sum_{j\in J} |a_j|^2. \end{align*} $$
Proof
![]() ${\mathcal V}$
is a frame, so for all finite sequences
${\mathcal V}$
is a frame, so for all finite sequences
![]() $ \{a_j\}_{j\in J}\subset \mathbb {C} $
, there is
$ \{a_j\}_{j\in J}\subset \mathbb {C} $
, there is
![]() $f\in H$
such that
$f\in H$
such that
![]() $f=\sum _{j\in J} a_j v_j.$
So,
$f=\sum _{j\in J} a_j v_j.$
So,
 $$ \begin{align*} \begin{aligned} ||f||^2&=\langle\sum_{j\in J} a_j v_j,f\rangle=\sum_{j\in J} a_j\langle v_j,f\rangle\\ &\leq \sqrt{\sum_{j\in J} |a_j|^2} \sqrt{\sum_{j\in J} |\langle v_j,f\rangle|^2}\leq \sqrt{\sum_{j\in J} |a_j|^2} \sqrt{B}||f||. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} ||f||^2&=\langle\sum_{j\in J} a_j v_j,f\rangle=\sum_{j\in J} a_j\langle v_j,f\rangle\\ &\leq \sqrt{\sum_{j\in J} |a_j|^2} \sqrt{\sum_{j\in J} |\langle v_j,f\rangle|^2}\leq \sqrt{\sum_{j\in J} |a_j|^2} \sqrt{B}||f||. \end{aligned} \end{align*} $$
Therefore,
 $$ \begin{align*}\Big\Vert \sum_{j\in J} a_j v_j \Big\Vert \leq \sqrt{\sum_{j\in J} |a_j|^2} \sqrt{B}.\\[-34pt] \end{align*} $$
$$ \begin{align*}\Big\Vert \sum_{j\in J} a_j v_j \Big\Vert \leq \sqrt{\sum_{j\in J} |a_j|^2} \sqrt{B}.\\[-34pt] \end{align*} $$
One more lemma that makes a connection between frames and bases is the following.
Lemma 2.2 If
![]() $E(\Lambda )$
is basis for
$E(\Lambda )$
is basis for
![]() $L^2(D)$
and
$L^2(D)$
and
![]() $D'\subset D$
, then
$D'\subset D$
, then
![]() $E(\Lambda )$
is a frame for
$E(\Lambda )$
is a frame for
![]() $L^2(D')$
with at least the same frame constants. In particular, if
$L^2(D')$
with at least the same frame constants. In particular, if
![]() $E(\Lambda )$
is an orthogonal basis for
$E(\Lambda )$
is an orthogonal basis for
![]() $L^2(D)$
, then it is a tight frame for
$L^2(D)$
, then it is a tight frame for
![]() $L^2(D')$
.
$L^2(D')$
.
Proof Let
![]() $E(\Lambda )$
is a basis for
$E(\Lambda )$
is a basis for
![]() $L^2(D),$
then for all
$L^2(D),$
then for all
![]() $w\in L^2(D)$
,
$w\in L^2(D)$
,
 $$ \begin{align*}A||w||^2\leq \sum_{j=1}^{\infty} |\langle w, v_j\rangle |^2\leq B ||w||^2. \end{align*} $$
$$ \begin{align*}A||w||^2\leq \sum_{j=1}^{\infty} |\langle w, v_j\rangle |^2\leq B ||w||^2. \end{align*} $$
Also, for any
![]() $f\in L^2(D'),$
there is
$f\in L^2(D'),$
there is
![]() $w\in L^2(D)$
such that
$w\in L^2(D)$
such that
![]() $f=w\chi _{D'}.$
So, the frame inequalities hold for any
$f=w\chi _{D'}.$
So, the frame inequalities hold for any
![]() $f\in L^2(D').$
Therefore,
$f\in L^2(D').$
Therefore,
![]() $E(\Lambda )$
is a frame for
$E(\Lambda )$
is a frame for
![]() $L^2(D')$
with at least the same frame constants.
$L^2(D')$
with at least the same frame constants.
An important characterization of Riesz bases is that they are bounded and unconditional Schäuder bases. See, e.g., [Reference Heil8].
Let
![]() $\vec v \in \mathbb {R}^d$
and
$\vec v \in \mathbb {R}^d$
and
![]() $\rho>0$
; we denote by
$\rho>0$
; we denote by
![]() $d_{\rho } D =\{ \rho x \ : \: x\in D\}$
and by
$d_{\rho } D =\{ \rho x \ : \: x\in D\}$
and by
![]() $ t_{\vec v} D = \{x+\vec v \ : \ x\in D\}$
the dilation and translation of D. Sometimes, we will write
$ t_{\vec v} D = \{x+\vec v \ : \ x\in D\}$
the dilation and translation of D. Sometimes, we will write
![]() $\vec v+D$
instead of
$\vec v+D$
instead of
![]() $t_{\vec v} D$
when there is no risk of confusion.
$t_{\vec v} D$
when there is no risk of confusion.
The following lemma can easily be proved with a change of variables in (2.1) and (2.2).
Lemma 2.3 Let
![]() $\vec v\in \mathbb {R}^d$
and
$\vec v\in \mathbb {R}^d$
and
![]() $\rho>0$
. The set
$\rho>0$
. The set
![]() ${\mathcal V}=\{ e^{2\pi i \langle x, \lambda _n\rangle }\}_{n\in \mathbb {Z}}$
is a Riesz basis for
${\mathcal V}=\{ e^{2\pi i \langle x, \lambda _n\rangle }\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(D)$
with constants A and B if and only if the set
$L^2(D)$
with constants A and B if and only if the set
![]() $\{ e^{2\pi i \langle x, \, \frac 1\rho \lambda _n \rangle }\}_{n\in \mathbb {Z}} $
is a Riesz basis for
$\{ e^{2\pi i \langle x, \, \frac 1\rho \lambda _n \rangle }\}_{n\in \mathbb {Z}} $
is a Riesz basis for
![]() $L^2(t_{\vec v}(d_{\rho } D ))$
with constants
$L^2(t_{\vec v}(d_{\rho } D ))$
with constants
![]() $A \rho ^{ d}$
and
$A \rho ^{ d}$
and
![]() $B \rho ^{ d}$
.
$B \rho ^{ d}$
.
2.1 Paley–Wiener and Kadec stability theorem
Bases in Banach spaces are stable, in the sense that small perturbations of a basis still produce bases.
One of the fundamental stability criteria, and historically the first, is due to Paley and Wiener in [Reference Paley and Wiener17].
Theorem 2.4 (Paley–Wiener theorem)
Let
![]() $\{x_n\}_{n\in \mathbb {N}}$
and
$\{x_n\}_{n\in \mathbb {N}}$
and
![]() $\{y_n\}_{n\in \mathbb {N}}$
be sequences in a Banach space X. Let
$\{y_n\}_{n\in \mathbb {N}}$
be sequences in a Banach space X. Let
![]() $\lambda $
be a real number
$\lambda $
be a real number
![]() $(0<\lambda <1)$
such that
$(0<\lambda <1)$
such that
 $$ \begin{align*} \left\lVert\sum_n a_n(x_n-y_n)\right\rVert\leq \lambda \left\lVert\sum_n a_n x_n\right\rVert \end{align*} $$
$$ \begin{align*} \left\lVert\sum_n a_n(x_n-y_n)\right\rVert\leq \lambda \left\lVert\sum_n a_n x_n\right\rVert \end{align*} $$
holds for any arbitrary finite set of scalars
![]() $\{a_n\}\subset \mathbb {C}.$
Then, if
$\{a_n\}\subset \mathbb {C}.$
Then, if
![]() $\{x_n\}$
is a basis, so is
$\{x_n\}$
is a basis, so is
![]() $\{y_n\}.$
Moreover, if
$\{y_n\}.$
Moreover, if
![]() $\{x_n\}$
has Riesz constants A and
$\{x_n\}$
has Riesz constants A and
![]() $B,$
then
$B,$
then
We will use the following important observation: if
![]() ${\mathcal {B}}=\{x_n\}_{n\in \mathbb {N}}$
is a bounded and unconditional basis in a Banach space
${\mathcal {B}}=\{x_n\}_{n\in \mathbb {N}}$
is a bounded and unconditional basis in a Banach space
![]() $(X, \ ||\ ||) $
, and
$(X, \ ||\ ||) $
, and
![]() $||\ ||_*$
is a norm equivalent to
$||\ ||_*$
is a norm equivalent to
![]() $||\ ||$
, then
$||\ ||$
, then
![]() ${\mathcal {B}}$
is also a bounded and unconditional basis in
${\mathcal {B}}$
is also a bounded and unconditional basis in
![]() $(X,\ || \ ||_*)$
. Note that two norms
$(X,\ || \ ||_*)$
. Note that two norms
![]() $||\ ||_*$
and
$||\ ||_*$
and
![]() $||\ ||$
are equivalent if there are two constants c and C such that for all elements of the space,
$||\ ||$
are equivalent if there are two constants c and C such that for all elements of the space,
![]() $c||x||_*\leq ||x||\leq C||x||_*.$
$c||x||_*\leq ||x||\leq C||x||_*.$
Let a set
![]() $\{f_n\}_{n\in \mathbb {N}}$
be a Riesz basis for
$\{f_n\}_{n\in \mathbb {N}}$
be a Riesz basis for
![]() $L^2(D)$
with norm
$L^2(D)$
with norm
![]() $ ||\ ||_2$
if
$ ||\ ||_2$
if
![]() $||\ ||_*$
is equivalent to
$||\ ||_*$
is equivalent to
![]() $||\ ||_2$
, then
$||\ ||_2$
, then
![]() $\{f_n\}_{n\in \mathbb {N}}$
is a bounded and unconditional basis of
$\{f_n\}_{n\in \mathbb {N}}$
is a bounded and unconditional basis of
![]() $(L^2(D), \ ||\ ||_*).$
So, if a sequence
$(L^2(D), \ ||\ ||_*).$
So, if a sequence
![]() $\{g_n\}_{n\in \mathbb {N}}\subset L^2(D)$
satisfies the conditions of the Paley–Wiener theorem with respect to the norm
$\{g_n\}_{n\in \mathbb {N}}\subset L^2(D)$
satisfies the conditions of the Paley–Wiener theorem with respect to the norm
![]() $||\ ||_*$
, i.e.,
$||\ ||_*$
, i.e.,
 $$ \begin{align*}\left\lVert\sum_n c_n(f_n-g_n)\right\rVert_*\leq \lambda \left\lVert\sum_n c_n f_n\right\rVert_* \end{align*} $$
$$ \begin{align*}\left\lVert\sum_n c_n(f_n-g_n)\right\rVert_*\leq \lambda \left\lVert\sum_n c_n f_n\right\rVert_* \end{align*} $$
with
![]() $0<\lambda <1,$
then
$0<\lambda <1,$
then
![]() $\{g_n\}_{n\in \mathbb {N}}$
is a bounded and unconditional basis of
$\{g_n\}_{n\in \mathbb {N}}$
is a bounded and unconditional basis of
![]() $(L^2(D), \ ||\ ||_*)$
and hence also of
$(L^2(D), \ ||\ ||_*)$
and hence also of
![]() $(L^2(D), \ ||\ || )$
. Thus,
$(L^2(D), \ ||\ || )$
. Thus,
![]() $\{g_n\}_{n\in \mathbb {N}}$
is a Riesz basis in
$\{g_n\}_{n\in \mathbb {N}}$
is a Riesz basis in
![]() $(L^2(D), \ ||\ || )$
. This observation proves the following lemma, which will be useful later on.
$(L^2(D), \ ||\ || )$
. This observation proves the following lemma, which will be useful later on.
Lemma 2.5 Let
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $D=\cup _{j=1}^m D_j\subset \mathbb {R}^d$
where
$D=\cup _{j=1}^m D_j\subset \mathbb {R}^d$
where
![]() $D_j\cap D_k=\emptyset .$
Let
$D_j\cap D_k=\emptyset .$
Let
![]() $\{g_n\}_{n\in \ N}$
be a Riesz basis for
$\{g_n\}_{n\in \ N}$
be a Riesz basis for
![]() $L^2(D)$
. Let
$L^2(D)$
. Let
![]() $ \{h_n\}_{n\in \mathbb {Z}} \subset L^2(D)$
be such that for every finite sequence
$ \{h_n\}_{n\in \mathbb {Z}} \subset L^2(D)$
be such that for every finite sequence
![]() $\{a_n\}\in \mathbb {C}$
,
$\{a_n\}\in \mathbb {C}$
,
 $$ \begin{align*}\sup_{j\leq m} \left\lVert\sum_n a_n(g_n-h_n)\right\rVert_{L^2(D_j)}\leq \alpha \sup_j \left\lVert\sum_n a_n g_n\right\rVert_{L^2(D_j)}. \end{align*} $$
$$ \begin{align*}\sup_{j\leq m} \left\lVert\sum_n a_n(g_n-h_n)\right\rVert_{L^2(D_j)}\leq \alpha \sup_j \left\lVert\sum_n a_n g_n\right\rVert_{L^2(D_j)}. \end{align*} $$
Then, the set
![]() $ \{h_n\}_{n\in \mathbb {Z}}$
is a Riesz basis for
$ \{h_n\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(D)$
.
$L^2(D)$
.
The celebrated Kadec stability theorem (also called Kadec’s
![]() $\frac 14$
-theorem) gives an optimal measure of how the standard orthonormal basis
$\frac 14$
-theorem) gives an optimal measure of how the standard orthonormal basis
![]() ${\mathcal E}=\{e^{2\pi i n x}\}_{n\in \mathbb {Z} }$
on the unit interval
${\mathcal E}=\{e^{2\pi i n x}\}_{n\in \mathbb {Z} }$
on the unit interval
![]() $[0,1]$
can be perturbed to still obtain an exponential basis.
$[0,1]$
can be perturbed to still obtain an exponential basis.
Theorem 2.6 Let
![]() $\Lambda = \{\lambda _n \}_{n\in \mathbb {Z}} $
be a sequence in
$\Lambda = \{\lambda _n \}_{n\in \mathbb {Z}} $
be a sequence in
![]() $\mathbb {R}$
for which
$\mathbb {R}$
for which
whenever
![]() $n\in \mathbb {Z}.$
Then,
$n\in \mathbb {Z}.$
Then,
![]() $ E(\Lambda )=\left \{e^{2\pi i {\lambda }_n x }\right \}_{ {\lambda }\in \Lambda }$
is an exponential basis for
$ E(\Lambda )=\left \{e^{2\pi i {\lambda }_n x }\right \}_{ {\lambda }\in \Lambda }$
is an exponential basis for
![]() $L^2(0,1)$
with frame constants
$L^2(0,1)$
with frame constants
![]() $A=\cos (\pi L)-\sin ( \pi L)$
and
$A=\cos (\pi L)-\sin ( \pi L)$
and
![]() $B= 2-\cos (\pi L)+\sin ( \pi L)$
. The constant
$B= 2-\cos (\pi L)+\sin ( \pi L)$
. The constant
![]() $\frac {1}{4}$
cannot be replaced by any larger constant.
$\frac {1}{4}$
cannot be replaced by any larger constant.
The theorem is proved using the Paley–Wiener theorem and a clever Fourier series expansion of the function
![]() $1- e^{2\pi i \delta x}$
. The quantity
$1- e^{2\pi i \delta x}$
. The quantity
plays an important part in the proof of the theorem, as well as in other generalizations. So, we can rewrite the frame constants of
![]() $E(\Lambda )$
as
$E(\Lambda )$
as
 $$ \begin{align*} \begin{split} A&= 1-D(L)=\cos(\pi L)-\sin( \pi L),\\ B&=1+D(L)= 2-\cos(\pi L)+\sin( \pi L). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} A&= 1-D(L)=\cos(\pi L)-\sin( \pi L),\\ B&=1+D(L)= 2-\cos(\pi L)+\sin( \pi L). \end{split} \end{align*} $$
Kadec’s theorem has been generalized to prove the stability of general exponential frames. See Theorem 1 in [Reference Balan2].
An important generalization of Kadec’s theorem is due to Avdonin [Reference Avdonin1].
Theorem 2.7 (Special version of Avdonin’s theorem)
Let
![]() $\lambda _n=n+\delta _n$
and suppose
$\lambda _n=n+\delta _n$
and suppose
![]() $\{\lambda _n\}_{n\in \mathbb {Z}}$
is separated, i.e.,
$\{\lambda _n\}_{n\in \mathbb {Z}}$
is separated, i.e.,
![]() $\inf _{n\neq k}|\lambda _n-\lambda _k|>0.$
If there exist a positive integer N and a positive real number
$\inf _{n\neq k}|\lambda _n-\lambda _k|>0.$
If there exist a positive integer N and a positive real number
![]() $\varepsilon <\frac 14$
such that
$\varepsilon <\frac 14$
such that
 $$ \begin{align} \left| \sum_{n=mN+1}^{(m+1)N} \delta_n\right|\leq \varepsilon N \end{align} $$
$$ \begin{align} \left| \sum_{n=mN+1}^{(m+1)N} \delta_n\right|\leq \varepsilon N \end{align} $$
for all integers
![]() $m,$
then the system
$m,$
then the system
![]() $\{e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
$\{e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2([0,1]).$
$L^2([0,1]).$
This special version of Avdonin’s theorem can be found in [Reference Seip20]. The condition (2.4) is hard to prove in the case when the sequence is not periodic. But, in our case, the following lemma will help.
Lemma 2.8 When g is Riemann integrable in
![]() $[0,1],$
and periodic of period
$[0,1],$
and periodic of period
![]() $1,$
and
$1,$
and
![]() $\beta $
is irrational, then
$\beta $
is irrational, then
 $$ \begin{align*} \lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N} g(n\beta) = \int_0^1 g(x) dx. \end{align*} $$
$$ \begin{align*} \lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N} g(n\beta) = \int_0^1 g(x) dx. \end{align*} $$
This lemma is Corollary 2.3 on page 110 in [Reference Stein and Shakarchi22].
2.2 Bases on disconnected domains
Let
![]() $E(\Lambda )$
be an exponential basis on a domain
$E(\Lambda )$
be an exponential basis on a domain
![]() $D\subset \mathbb {R}^d$
. If D is partitioned into disjoint sets
$D\subset \mathbb {R}^d$
. If D is partitioned into disjoint sets
![]() $D_1,\ldots , D_m,\ldots $
, which are then translated with translations
$D_1,\ldots , D_m,\ldots $
, which are then translated with translations
![]() $\tau _1,\, \dots \tau _m,\ldots $
in such a way that the translated pieces do not intersect, then in general
$\tau _1,\, \dots \tau _m,\ldots $
in such a way that the translated pieces do not intersect, then in general
![]() $E(\Lambda )$
is not a basis on the “broken domain”
$E(\Lambda )$
is not a basis on the “broken domain”
![]() $\tilde {D} = D_1+\tau _1\cup \cdots \cup D_m+\tau _m\cup \cdots .$
The following lemma shows how a basis
$\tilde {D} = D_1+\tau _1\cup \cdots \cup D_m+\tau _m\cup \cdots .$
The following lemma shows how a basis
![]() $E(\Lambda )$
for
$E(\Lambda )$
for
![]() $L^2(D)$
can be transformed into a basis for
$L^2(D)$
can be transformed into a basis for
![]() $L^2(\tilde D)$
.
$L^2(\tilde D)$
.
Lemma 2.9 Let
![]() $D\subset \mathbb {R}^d$
be measurable, with
$D\subset \mathbb {R}^d$
be measurable, with
![]() $|D|<\infty $
; let for
$|D|<\infty $
; let for
![]() $m\in \mathbb {N}\cup \{\infty \},$
we have
$m\in \mathbb {N}\cup \{\infty \},$
we have
![]() $ D=\bigcup _{j=0}^{m} D_j$
, with
$ D=\bigcup _{j=0}^{m} D_j$
, with
![]() $|D_j|>0$
for all j and
$|D_j|>0$
for all j and
![]() $k\ D_k\cap D_j=\emptyset $
when
$k\ D_k\cap D_j=\emptyset $
when
![]() $k\ne j$
. Let
$k\ne j$
. Let
![]() $\tau _j$
be translations such that
$\tau _j$
be translations such that
![]() $ \tau _j(D_j) \cap \tau _k(D_k) =\emptyset $
when
$ \tau _j(D_j) \cap \tau _k(D_k) =\emptyset $
when
![]() $k\ne j$
. Let
$k\ne j$
. Let
![]() $\tilde D = \bigcup _{j=1}^m \tau _j(D_j) $
. If
$\tilde D = \bigcup _{j=1}^m \tau _j(D_j) $
. If
![]() ${\mathcal {B}}=\{\psi _n(x)\}_{n\in \mathbb {N}} \subset L^2(D)$
is a Riesz basis for
${\mathcal {B}}=\{\psi _n(x)\}_{n\in \mathbb {N}} \subset L^2(D)$
is a Riesz basis for
![]() $L^2(D)$
, then
$L^2(D)$
, then
 $$ \begin{align*}\tilde {\mathcal{B}} =\Bigg\{\sum_{j=1}^m \chi_{ \tau_j(D_j)}\psi_n(\tau_j^{-1}x)\Bigg\}_{n\in\mathbb{N}}\end{align*} $$
$$ \begin{align*}\tilde {\mathcal{B}} =\Bigg\{\sum_{j=1}^m \chi_{ \tau_j(D_j)}\psi_n(\tau_j^{-1}x)\Bigg\}_{n\in\mathbb{N}}\end{align*} $$
is a Riesz basis for
![]() $L^2(\tilde D)$
with the same frame constants.
$L^2(\tilde D)$
with the same frame constants.
Proof With some abuse of notation, we will let
![]() $\tau _j(x)=x+\tau _j $
and
$\tau _j(x)=x+\tau _j $
and
![]() $\tau _j(D_j)=D^{\prime }_j$
. Thus,
$\tau _j(D_j)=D^{\prime }_j$
. Thus,
![]() $\tilde D=\bigcup _{j=1}^m D^{\prime }_j$
.
$\tilde D=\bigcup _{j=1}^m D^{\prime }_j$
.
Define the operator
![]() $T: L^2(D)\rightarrow L^2(\tilde D)$
by
$T: L^2(D)\rightarrow L^2(\tilde D)$
by
![]() $T^{-1}(f)(x)=\sum _{k=1}^{m} f(x-\tau _k )\chi _{D_k}.$
This is a linear transformation. We can also check that T is invertible, and its inverse is the operator
$T^{-1}(f)(x)=\sum _{k=1}^{m} f(x-\tau _k )\chi _{D_k}.$
This is a linear transformation. We can also check that T is invertible, and its inverse is the operator
![]() $T^{-1}: L^2(\tilde D)\rightarrow L^2 ( D)$
defined as
$T^{-1}: L^2(\tilde D)\rightarrow L^2 ( D)$
defined as
![]() $T^{-1}(f)(x)=\sum _{k=1}^{m} f(x+\tau _k )\chi _{D^{\prime }_k}.$
Let us show that T (and also
$T^{-1}(f)(x)=\sum _{k=1}^{m} f(x+\tau _k )\chi _{D^{\prime }_k}.$
Let us show that T (and also
![]() $T^{-1}$
) are isometry. Indeed, for every
$T^{-1}$
) are isometry. Indeed, for every
![]() $f\in L^2(D)$
,
$f\in L^2(D)$
,
 $$ \begin{align*} \begin{aligned} \left\lVert T(f)\right\rVert_{L^2(\tilde D)}^2&=\sum_{k=1}^m\left\lVert T(f)\right\rVert_{ L^2(D_k') }^2 =\sum_{k=1}^m \int_{\tau_k+D_k } |f(x-\tau_k)|^2dx\\ & =\sum_{k=1}^m \int_{D_k } |f(x)|^2dx= ||f||_{L^2(D)}^2, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\lVert T(f)\right\rVert_{L^2(\tilde D)}^2&=\sum_{k=1}^m\left\lVert T(f)\right\rVert_{ L^2(D_k') }^2 =\sum_{k=1}^m \int_{\tau_k+D_k } |f(x-\tau_k)|^2dx\\ & =\sum_{k=1}^m \int_{D_k } |f(x)|^2dx= ||f||_{L^2(D)}^2, \end{aligned} \end{align*} $$
where the third equality comes from a change of variables in the integrals. An invertible isometry maps bases into bases, and the frame constants are the same. Since
![]() $\tilde {\mathcal {B}}= T({\mathcal {B}})$
, we have proved that
$\tilde {\mathcal {B}}= T({\mathcal {B}})$
, we have proved that
![]() $\tilde {\mathcal {B}}$
is a basis for
$\tilde {\mathcal {B}}$
is a basis for
![]() $L^2(\tilde D).$
$L^2(\tilde D).$
Remark 2.10 Let
![]() $\{\lambda _n\}_{n\in \mathbb {Z}}\subset \mathbb {R}^d$
,
$\{\lambda _n\}_{n\in \mathbb {Z}}\subset \mathbb {R}^d$
,
![]() $\{b_k\}_{k=0}^{m-1}\subset \mathbb {R}^d,$
with
$\{b_k\}_{k=0}^{m-1}\subset \mathbb {R}^d,$
with
![]() $m\in \mathbb {N}\cup \{\infty \}$
, and D and
$m\in \mathbb {N}\cup \{\infty \}$
, and D and
![]() $\tilde D,$
as in Lemma 2.9. Also, let
$\tilde D,$
as in Lemma 2.9. Also, let
![]() $ w_n= \sum _{k=0}^{m-1} e^{2\pi i b_k \lambda _n}\chi _{\tilde D_k}.$
The set
$ w_n= \sum _{k=0}^{m-1} e^{2\pi i b_k \lambda _n}\chi _{\tilde D_k}.$
The set
![]() $ \{e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
$ \{e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(\tilde D) $
if and only if the set
$L^2(\tilde D) $
if and only if the set
![]() $ \{ w_ne^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
$ \{ w_ne^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(D) $
. Moreover, those two bases have the same Riesz constants. We can also see that the set
$L^2(D) $
. Moreover, those two bases have the same Riesz constants. We can also see that the set
![]() $ \{ \overline { w_n}e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
$ \{ \overline { w_n}e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(D) $
if and only if the set
$L^2(D) $
if and only if the set
![]() $ \{ e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
$ \{ e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(\tilde D) $
. Moreover, those two bases have the same Riesz constants.
$L^2(\tilde D) $
. Moreover, those two bases have the same Riesz constants.
If we replace D by
![]() $J,$
when
$J,$
when
with
![]() $J_j=[a_{j}+b_j,a_{j+1}+b_j),$
as in (1.1), then we obtain a special case of Lemma 2.9.
$J_j=[a_{j}+b_j,a_{j+1}+b_j),$
as in (1.1), then we obtain a special case of Lemma 2.9.
Lemma 2.11 For m finite or infinite, the sequence
![]() $\{g_n\}_{n\in \mathbb {Z}},$
where
$\{g_n\}_{n\in \mathbb {Z}},$
where
 $$ \begin{align*}g_n=\sum_{k=0}^{m} e^{2\pi i x \lambda_n}e^{2\pi i b_k \lambda_n}\chi_{J_k},\end{align*} $$
$$ \begin{align*}g_n=\sum_{k=0}^{m} e^{2\pi i x \lambda_n}e^{2\pi i b_k \lambda_n}\chi_{J_k},\end{align*} $$
is a Riesz basis for
![]() $L^2(J)$
if and only if
$L^2(J)$
if and only if
![]() ${\mathcal {B}}=\{e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
${\mathcal {B}}=\{e^{2\pi i x \lambda _n}\}_{n\in \mathbb {Z}}$
is a Riesz basis for
![]() $L^2(I).$
Moreover, two bases
$L^2(I).$
Moreover, two bases
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() $\{g_n\}$
have the same Riesz constants. Conversely, the set
$\{g_n\}$
have the same Riesz constants. Conversely, the set
![]() $\{\overset {\sim }{g}_n\}_{n\in \mathbb {Z}},$
where
$\{\overset {\sim }{g}_n\}_{n\in \mathbb {Z}},$
where
 $$ \begin{align*}\overset{\sim}{g}_n=\sum_{k=0}^{m} e^{2\pi i x \lambda_n}e^{-2\pi i b_k \lambda_n}\chi_{I_k},\end{align*} $$
$$ \begin{align*}\overset{\sim}{g}_n=\sum_{k=0}^{m} e^{2\pi i x \lambda_n}e^{-2\pi i b_k \lambda_n}\chi_{I_k},\end{align*} $$
is a Riesz basis for
![]() $L^2(I)$
if and only if
$L^2(I)$
if and only if
![]() ${\mathcal {B}}$
is a Riesz basis for
${\mathcal {B}}$
is a Riesz basis for
![]() $L^2(J).$
Moreover, two bases
$L^2(J).$
Moreover, two bases
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() $\{\tilde g_n\}$
have the same Riesz constants.
$\{\tilde g_n\}$
have the same Riesz constants.
A version of Lemma 2.11 is also in [Reference De Carli and Kumar5].
3 Proofs of the main results
In this section, we will prove our main results. But first, we remind the reader that
![]() ${\mathcal {B}}^* =\{e^{2\pi i x(n+\delta _n^*)}\}_{n\in \mathbb {Z}},$
where
${\mathcal {B}}^* =\{e^{2\pi i x(n+\delta _n^*)}\}_{n\in \mathbb {Z}},$
where
 $$ \begin{align*}\delta_n^*= \begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12,\\ \end{cases} \end{align*} $$
$$ \begin{align*}\delta_n^*= \begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12,\\ \end{cases} \end{align*} $$
for some
![]() $\beta>0$
(see (1.4) and (4.5)).
$\beta>0$
(see (1.4) and (4.5)).
3.1 A useful lemma
Lemma 3.1 Let
![]() $\beta \ge 1.$
Then
$\beta \ge 1.$
Then
![]() ${\mathcal {B}}^*$
is an exponential basis for
${\mathcal {B}}^*$
is an exponential basis for
![]() $L^2([0,1]).$
$L^2([0,1]).$
Proof First, we let
![]() $\beta>2.$
Then
$\beta>2.$
Then
 $$ \begin{align*} \sup_{\beta\in\mathbb{Z}}|\delta_n^*|= \sup_{\beta\in\mathbb{Z}}\left|\frac{\operatorname{dist}{(\mathbb{Z},\beta n)}}{\beta}\right|\leq\frac{1}{2\beta}< \frac{1}{4}. \end{align*} $$
$$ \begin{align*} \sup_{\beta\in\mathbb{Z}}|\delta_n^*|= \sup_{\beta\in\mathbb{Z}}\left|\frac{\operatorname{dist}{(\mathbb{Z},\beta n)}}{\beta}\right|\leq\frac{1}{2\beta}< \frac{1}{4}. \end{align*} $$
So, by Theorem 2.6,
![]() $\left \{e^{2 \pi i x (n + \delta _n^*)}\right \}_{n\in \mathbb {Z}}$
is an exponential basis for
$\left \{e^{2 \pi i x (n + \delta _n^*)}\right \}_{n\in \mathbb {Z}}$
is an exponential basis for
![]() $L^2([0,1]).$
$L^2([0,1]).$
Next, let
![]() $1\leq \beta \leq 2$
and
$1\leq \beta \leq 2$
and
![]() $\beta \in \mathbb {Q}.$
First, trivial case with
$\beta \in \mathbb {Q}.$
First, trivial case with
![]() $\beta =1$
or
$\beta =1$
or
![]() $\beta =2.$
In this case,
$\beta =2.$
In this case,
![]() $\delta ^*_n=0$
for all
$\delta ^*_n=0$
for all
![]() $n.$
So,
$n.$
So,
![]() ${\mathcal {B}}^*=\left \{e^{2 \pi i x n}\right \}_{n\in \mathbb {Z}} $
, the standard basis for
${\mathcal {B}}^*=\left \{e^{2 \pi i x n}\right \}_{n\in \mathbb {Z}} $
, the standard basis for
![]() $L^2([0,1]).$
Now, let
$L^2([0,1]).$
Now, let
![]() $1< \beta < 2$
and
$1< \beta < 2$
and
![]() $\beta \in \mathbb {Q},$
so there are two integers p and q such that
$\beta \in \mathbb {Q},$
so there are two integers p and q such that
![]() $\beta =\frac {p}{q}.$
We are going to use Theorem 2.7, so we need to check if
$\beta =\frac {p}{q}.$
We are going to use Theorem 2.7, so we need to check if
![]() $\{\lambda _n\}_{n\in \mathbb {Z}}=\{n+\delta ^*_n\}_{n\in \mathbb {Z}}$
is separated and if there exist a positive integer N and a positive real number
$\{\lambda _n\}_{n\in \mathbb {Z}}=\{n+\delta ^*_n\}_{n\in \mathbb {Z}}$
is separated and if there exist a positive integer N and a positive real number
![]() $\varepsilon <\frac 14$
such that
$\varepsilon <\frac 14$
such that
 $$ \begin{align*} \left| \sum_{n=mN+1}^{(m+1)N} \delta_n^*\right|\leq \varepsilon N \end{align*} $$
$$ \begin{align*} \left| \sum_{n=mN+1}^{(m+1)N} \delta_n^*\right|\leq \varepsilon N \end{align*} $$
for all integers m (see (2.4)). For all
![]() $n\in \mathbb {Z}$
, we compare
$n\in \mathbb {Z}$
, we compare
![]() $\lambda _n$
and
$\lambda _n$
and
![]() $\lambda _{n+1}$
$\lambda _{n+1}$
 $$ \begin{align*} \begin{split} \lambda_{n}&=n+\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{ \beta n \} \geq \frac12 \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12\\ \end{cases}\leq n+\frac{1}{2b},\\ \lambda_{n+1}&=n+1+\begin{cases} \frac{\lfloor \beta (n+1) \rfloor+1}{\beta}-n-1, & \text{if } \{ \beta (n+1) \} \geq \frac12 \\ \frac{\lfloor \beta (n+1) \rfloor}{\beta}-n-1, & \text{if } \{\beta(n+1)\} < \frac12\\ \end{cases}\geq n+1-\frac{1}{2\beta}>\lambda_n.\\ \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \lambda_{n}&=n+\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{ \beta n \} \geq \frac12 \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12\\ \end{cases}\leq n+\frac{1}{2b},\\ \lambda_{n+1}&=n+1+\begin{cases} \frac{\lfloor \beta (n+1) \rfloor+1}{\beta}-n-1, & \text{if } \{ \beta (n+1) \} \geq \frac12 \\ \frac{\lfloor \beta (n+1) \rfloor}{\beta}-n-1, & \text{if } \{\beta(n+1)\} < \frac12\\ \end{cases}\geq n+1-\frac{1}{2\beta}>\lambda_n.\\ \end{split} \end{align*} $$
So, the sequence
![]() $\{\lambda _n\}_{n\in \mathbb {Z}}$
is increasing. Moreover,
$\{\lambda _n\}_{n\in \mathbb {Z}}$
is increasing. Moreover,
 $$ \begin{align*} \begin{split} \sup_{n\in\mathbb{Z}}|\lambda_{n+1}-\lambda_n|&\geq n+1-\frac{1}{2\beta} - \left(n+\frac{1}{2\beta}\right)= 1- \frac1\beta>0. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \sup_{n\in\mathbb{Z}}|\lambda_{n+1}-\lambda_n|&\geq n+1-\frac{1}{2\beta} - \left(n+\frac{1}{2\beta}\right)= 1- \frac1\beta>0. \end{split} \end{align*} $$
Therefore,
![]() $\{\lambda _n\}_{n\in \mathbb {Z}}$
is separated.
$\{\lambda _n\}_{n\in \mathbb {Z}}$
is separated.
Next, we observe that for all
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
 $$ \begin{align*} \begin{aligned} \delta^*_{n+q} &= \begin{cases} \frac{\lfloor \frac{p}{q} (n+q) \rfloor+1}{\frac{p}{q}}- n -q = \frac{\lfloor \frac{p}{q} n \rfloor + p+1}{\frac{p}{q}}-n-q, & \text{if } \left\{ \frac{p}{q} (n-q) \right\} \geq \frac12, \\ \frac{\lfloor \frac{p}{q} (n+q) \rfloor}{\frac{p}{q}}- n -q = \frac{\lfloor \frac{p}{q} n \rfloor + p}{\frac{p}{q}}-n-q, & \text{if } \left\{ \frac{p}{q} (n-q) \right\} < \frac12,\\ \end{cases}\\ &= \begin{cases} \frac{\lfloor \frac{p}{q} n \rfloor+1}{\frac{p}{q}}- n, & \text{if } \left\{ \frac{p}{q} n \right\} \geq \frac12,\\ \frac{\lfloor \frac{p}{q} n \rfloor}{\frac{p}{q}}- n, & \text{if } \left\{ \frac{p}{q} n \right\} < \frac12.\\ \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \delta^*_{n+q} &= \begin{cases} \frac{\lfloor \frac{p}{q} (n+q) \rfloor+1}{\frac{p}{q}}- n -q = \frac{\lfloor \frac{p}{q} n \rfloor + p+1}{\frac{p}{q}}-n-q, & \text{if } \left\{ \frac{p}{q} (n-q) \right\} \geq \frac12, \\ \frac{\lfloor \frac{p}{q} (n+q) \rfloor}{\frac{p}{q}}- n -q = \frac{\lfloor \frac{p}{q} n \rfloor + p}{\frac{p}{q}}-n-q, & \text{if } \left\{ \frac{p}{q} (n-q) \right\} < \frac12,\\ \end{cases}\\ &= \begin{cases} \frac{\lfloor \frac{p}{q} n \rfloor+1}{\frac{p}{q}}- n, & \text{if } \left\{ \frac{p}{q} n \right\} \geq \frac12,\\ \frac{\lfloor \frac{p}{q} n \rfloor}{\frac{p}{q}}- n, & \text{if } \left\{ \frac{p}{q} n \right\} < \frac12.\\ \end{cases} \end{aligned} \end{align*} $$
So,
![]() $\delta ^*_n=\delta ^*_{n+q}$
and we also observe that
$\delta ^*_n=\delta ^*_{n+q}$
and we also observe that
![]() $\delta ^*_q=0.$
Thus, in order to apply (2.4), it is enough to consider
$\delta ^*_q=0.$
Thus, in order to apply (2.4), it is enough to consider
![]() $\left |\sum _{n=1}^{q-1} \delta ^*_n \right |.$
Now, for all
$\left |\sum _{n=1}^{q-1} \delta ^*_n \right |.$
Now, for all
![]() $n=1,\ldots ,\lfloor \frac {q}{2}\rfloor $
,
$n=1,\ldots ,\lfloor \frac {q}{2}\rfloor $
,
 $$ \begin{align*} \begin{aligned} \delta^*_{q-n} &= \begin{cases} \frac{\lfloor \frac{p}{q} (q-n) \rfloor+1}{\frac{p}{q}}- q +n = \frac{\lfloor -\frac{p}{q} n \rfloor + p + 1}{\frac{p}{q}}-q+n, & \text{if } \left\{ \frac{p}{q} (q-n) \right\} \geq \frac12, \\ \frac{\lfloor \frac{p}{q} (q-n) \rfloor}{\frac{p}{q}}- q +n = \frac{\lfloor -\frac{p}{q} n \rfloor + p}{\frac{p}{q}}-q+n, & \text{if } \left\{ \frac{p}{q} (q-n) \right\} < \frac12,\\ \end{cases}\\ &= \begin{cases} -\frac{\lfloor \frac{p}{q} n \rfloor+1}{\frac{p}{q}}+ n, & \text{if } \left\{ \frac{p}{q} n \right\} \geq \frac12,\\ -\frac{\lfloor \frac{p}{q} n \rfloor}{\frac{p}{q}}+ n, & \text{if } \left\{ \frac{p}{q} n \right\} < \frac12.\\ \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \delta^*_{q-n} &= \begin{cases} \frac{\lfloor \frac{p}{q} (q-n) \rfloor+1}{\frac{p}{q}}- q +n = \frac{\lfloor -\frac{p}{q} n \rfloor + p + 1}{\frac{p}{q}}-q+n, & \text{if } \left\{ \frac{p}{q} (q-n) \right\} \geq \frac12, \\ \frac{\lfloor \frac{p}{q} (q-n) \rfloor}{\frac{p}{q}}- q +n = \frac{\lfloor -\frac{p}{q} n \rfloor + p}{\frac{p}{q}}-q+n, & \text{if } \left\{ \frac{p}{q} (q-n) \right\} < \frac12,\\ \end{cases}\\ &= \begin{cases} -\frac{\lfloor \frac{p}{q} n \rfloor+1}{\frac{p}{q}}+ n, & \text{if } \left\{ \frac{p}{q} n \right\} \geq \frac12,\\ -\frac{\lfloor \frac{p}{q} n \rfloor}{\frac{p}{q}}+ n, & \text{if } \left\{ \frac{p}{q} n \right\} < \frac12.\\ \end{cases} \end{aligned} \end{align*} $$
It means that
![]() $\delta ^*_n + \delta ^*_{q-n}=0.$
Moreover, if q is even, then
$\delta ^*_n + \delta ^*_{q-n}=0.$
Moreover, if q is even, then
![]() $\delta ^*_{\frac {q}{2}}+\delta ^*_{\frac {q}{2}}=0,$
and then
$\delta ^*_{\frac {q}{2}}+\delta ^*_{\frac {q}{2}}=0,$
and then
![]() $\delta ^*_{\frac {q}{2}}=0.$
Thus,
$\delta ^*_{\frac {q}{2}}=0.$
Thus,
 $$ \begin{align*}\left|\sum_{n=1}^{q-1} \delta^*_n \right| = 0. \end{align*} $$
$$ \begin{align*}\left|\sum_{n=1}^{q-1} \delta^*_n \right| = 0. \end{align*} $$
If q is odd, then
 $$ \begin{align*} \begin{aligned} \left|\sum_{n=1}^{q} \delta^*_n \right| &= |\delta^*_{\frac{q+1}{2}}| =\left|\begin{cases} \frac{\lfloor \frac{p}{2} \rfloor+1}{\frac{p}{q}}-\frac{q}{2} & \text{if } \left\{ \frac{p}{2} \right\} \geq \frac12 \\ \frac{\lfloor \frac{p}{2} \rfloor}{\frac{p}{q}}-\frac{q}{2} & \text{if } \left\{ \frac{p}{2} \right\} < \frac12\\ \end{cases} \right|= \begin{cases} 0, & \text{if } p \text{ is even} \\ \frac{1}{2b}, & \text{if } p \text{ is odd}\\ \end{cases}< \frac{1}{4}<\frac{q}{4}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left|\sum_{n=1}^{q} \delta^*_n \right| &= |\delta^*_{\frac{q+1}{2}}| =\left|\begin{cases} \frac{\lfloor \frac{p}{2} \rfloor+1}{\frac{p}{q}}-\frac{q}{2} & \text{if } \left\{ \frac{p}{2} \right\} \geq \frac12 \\ \frac{\lfloor \frac{p}{2} \rfloor}{\frac{p}{q}}-\frac{q}{2} & \text{if } \left\{ \frac{p}{2} \right\} < \frac12\\ \end{cases} \right|= \begin{cases} 0, & \text{if } p \text{ is even} \\ \frac{1}{2b}, & \text{if } p \text{ is odd}\\ \end{cases}< \frac{1}{4}<\frac{q}{4}, \end{aligned} \end{align*} $$
because
![]() $q>1.$
Therefore, using Theorem 2.7, we conclude that
$q>1.$
Therefore, using Theorem 2.7, we conclude that
![]() $\left \{e^{2 \pi x (n + \delta _n^*)}\right \}_{n\in \mathbb {Z}}$
is an exponential basis for
$\left \{e^{2 \pi x (n + \delta _n^*)}\right \}_{n\in \mathbb {Z}}$
is an exponential basis for
![]() $L^2([0,1]).$
$L^2([0,1]).$
Next, we consider the case when
![]() $1<\beta <2$
is irrational. We can rewrite our sequence in the form
$1<\beta <2$
is irrational. We can rewrite our sequence in the form
 $$ \begin{align*}\delta_n^* = \frac{g(n \beta)}{\beta}, \end{align*} $$
$$ \begin{align*}\delta_n^* = \frac{g(n \beta)}{\beta}, \end{align*} $$
where
 $$ \begin{align*}g(x)=\begin{cases} 1 - \{ x \}, & \text{if } \{ x \} \geq \frac12, \\ - \{ x \}, & \text{if } \{ x \} < \frac12.\\ \end{cases} \end{align*} $$
$$ \begin{align*}g(x)=\begin{cases} 1 - \{ x \}, & \text{if } \{ x \} \geq \frac12, \\ - \{ x \}, & \text{if } \{ x \} < \frac12.\\ \end{cases} \end{align*} $$
g is Riemann integrable in
![]() $[0,1],$
and periodic of period
$[0,1],$
and periodic of period
![]() $1.$
Moreover,
$1.$
Moreover,
So, by Lemma 2.8,
 $$ \begin{align*}\lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N} g(n\beta)=0. \end{align*} $$
$$ \begin{align*}\lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N} g(n\beta)=0. \end{align*} $$
Moreover, by simple translation, we can get that for all
![]() $m\in \mathbb {Z}$
,
$m\in \mathbb {Z}$
,
 $$ \begin{align*}\lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=mN+1}^{(m+1)N} \frac{g(n\beta)}{\beta}=0. \end{align*} $$
$$ \begin{align*}\lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=mN+1}^{(m+1)N} \frac{g(n\beta)}{\beta}=0. \end{align*} $$
It means that for any
![]() $\varepsilon <\frac {1}{4},$
there is an
$\varepsilon <\frac {1}{4},$
there is an
![]() $N_0$
such that for all
$N_0$
such that for all
![]() $m\in \mathbb {Z}$
and for all
$m\in \mathbb {Z}$
and for all
![]() $N>N_0$
,
$N>N_0$
,
 $$ \begin{align*}\left|\frac{1}{N}\sum_{n=mN+1}^{(m+1)N} \frac{g(n\beta)}{\beta}\right| =\left|\frac{1}{N}\sum_{n=mN+1}^{(m+1)N} \delta_n^*\right| <\varepsilon. \end{align*} $$
$$ \begin{align*}\left|\frac{1}{N}\sum_{n=mN+1}^{(m+1)N} \frac{g(n\beta)}{\beta}\right| =\left|\frac{1}{N}\sum_{n=mN+1}^{(m+1)N} \delta_n^*\right| <\varepsilon. \end{align*} $$
Therefore, using Theorem 2.7, we conclude that
![]() $\left \{e^{2 \pi x (n + \delta _n^*)}\right \}_{n\in \mathbb {Z}}$
is an exponential basis for
$\left \{e^{2 \pi x (n + \delta _n^*)}\right \}_{n\in \mathbb {Z}}$
is an exponential basis for
![]() $L^2([0,1]).$
$L^2([0,1]).$
Remark 3.2 Since we proved that
![]() $\delta _n^*$
is periodic when
$\delta _n^*$
is periodic when
![]() $1\leq \beta \leq 2$
and
$1\leq \beta \leq 2$
and
![]() $\beta \in \mathbb {Q},$
we could also have used Corollary 3.1 from [Reference De Carli4] to conclude that
$\beta \in \mathbb {Q},$
we could also have used Corollary 3.1 from [Reference De Carli4] to conclude that
![]() ${\mathcal {B}}^*$
is an exponential basis for
${\mathcal {B}}^*$
is an exponential basis for
![]() $L^2([0,1]).$
$L^2([0,1]).$
Remark 3.3 If
![]() $\beta>2$
, then Theorem 2.6 shows that the frame constants of the basis are
$\beta>2$
, then Theorem 2.6 shows that the frame constants of the basis are
![]() $A=\cos (\pi L)-\sin ( \pi L)$
and
$A=\cos (\pi L)-\sin ( \pi L)$
and
![]() $B= 2-\cos (\pi L)+\sin ( \pi L)$
, where
$B= 2-\cos (\pi L)+\sin ( \pi L)$
, where
![]() $L=\sup _{n\in \mathbb {Z}}|\delta _n|.$
$L=\sup _{n\in \mathbb {Z}}|\delta _n|.$
3.2 Proof of Theorem 1.1
Proof Let m be infinite or finite. By Lemma 3.1,
![]() ${\mathcal {B}}^*$
is an exponential basis for
${\mathcal {B}}^*$
is an exponential basis for
![]() $L^2(I)$
with the Riesz constants A and
$L^2(I)$
with the Riesz constants A and
![]() $B.$
We can obtain a Riesz basis
$B.$
We can obtain a Riesz basis
![]() $\{g_n\}_{n\in \mathbb {Z}}$
for
$\{g_n\}_{n\in \mathbb {Z}}$
for
![]() $L^2(J)$
using Lemma 2.11, where
$L^2(J)$
using Lemma 2.11, where
![]() $g_n=\sum _{k=0}^{m-1} e^{2\pi i (x-b_k) (n+\delta _n^*)}\chi _{J_k}.$
Next, we use the Paley–Wiener theorem to show that
$g_n=\sum _{k=0}^{m-1} e^{2\pi i (x-b_k) (n+\delta _n^*)}\chi _{J_k}.$
Next, we use the Paley–Wiener theorem to show that
![]() ${\mathcal {B}}^*$
is a basis for
${\mathcal {B}}^*$
is a basis for
![]() $L^2(J)$
. So, we need to show that there is
$L^2(J)$
. So, we need to show that there is
![]() $0\leq \alpha <1$
such that for all sequence
$0\leq \alpha <1$
such that for all sequence
![]() $\{a_n\}$
with the property
$\{a_n\}$
with the property
![]() $\sum |a_n|^2= 1$
,
$\sum |a_n|^2= 1$
,
Using a simple substitution and the Riesz constants of the basis
![]() ${\mathcal {B}}^*$
we, can estimate the right-hand side of the inequality (3.1)
${\mathcal {B}}^*$
we, can estimate the right-hand side of the inequality (3.1)
For the left-hand side, using the definition of
![]() $g_n$
and Minkowski’s inequality,
$g_n$
and Minkowski’s inequality,
 $$ \begin{align*} \begin{aligned} ||\sum a_n (g_n-e^{2\pi ix (n+\delta_n^*)}) ||^2_{L^2(J)} &\leq \sum_{k=1}^{m-1} ||\sum a_n (e^{2\pi i(x-b_k) (n+\delta_n^*)}-e^{2\pi ix (n+\delta_n^*)}) ||^2_{L^2(J_k)}\\ &= \sum_{k=1}^{m-1} ||\sum a_n (e^{-2\pi ib_k (n+\delta_n^*)}-1) e^{2\pi ix (n+\delta_n^*)} ||^2_{L^2(J_k)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} ||\sum a_n (g_n-e^{2\pi ix (n+\delta_n^*)}) ||^2_{L^2(J)} &\leq \sum_{k=1}^{m-1} ||\sum a_n (e^{2\pi i(x-b_k) (n+\delta_n^*)}-e^{2\pi ix (n+\delta_n^*)}) ||^2_{L^2(J_k)}\\ &= \sum_{k=1}^{m-1} ||\sum a_n (e^{-2\pi ib_k (n+\delta_n^*)}-1) e^{2\pi ix (n+\delta_n^*)} ||^2_{L^2(J_k)}. \end{aligned} \end{align*} $$
Next, we recall that
 $$ \begin{align*} \delta_n^*=\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \delta_n^*=\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}-n, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta}-n, & \text{if } \{\beta n\} < \frac12.\\ \end{cases} \end{align*} $$
It means that for each
![]() $n\in \mathbb {Z}$
, we can find
$n\in \mathbb {Z}$
, we can find
![]() $M_{n}\in \mathbb {Z}$
such that
$M_{n}\in \mathbb {Z}$
such that
![]() $\delta _n^*=\frac {M_{n}}{\beta }-n.$
Thus, for all
$\delta _n^*=\frac {M_{n}}{\beta }-n.$
Thus, for all
![]() $k=1,\ldots ,m-1,$
$k=1,\ldots ,m-1,$
because
![]() $\frac {b_k}{\beta }\in \mathbb {Z}$
for
$\frac {b_k}{\beta }\in \mathbb {Z}$
for
![]() $k=1,\ldots ,m-1.$
So,
$k=1,\ldots ,m-1.$
So,
and the inequality (3.1) holds. Therefore,
![]() ${\mathcal {B}}^*$
is an exponential basis for
${\mathcal {B}}^*$
is an exponential basis for
![]() $L^2(J)$
with Riesz constants A and
$L^2(J)$
with Riesz constants A and
![]() $B.$
$B.$
3.3 Proof of Theorem 1.2
In [Reference Pfander, Shauna and Walnut19], the reader can find the following result.
Theorem 3.4 Let
![]() $\Delta>0$
and
$\Delta>0$
and
![]() $S\subset [0,\Delta ].$
Suppose that for some
$S\subset [0,\Delta ].$
Suppose that for some
![]() $\Lambda \subset \frac {1}{\Delta }\mathbb {Z}$
,
$\Lambda \subset \frac {1}{\Delta }\mathbb {Z}$
,
![]() ${\mathcal E}(\Lambda )$
is a Riesz basis for
${\mathcal E}(\Lambda )$
is a Riesz basis for
![]() $L^2(S).$
Then
$L^2(S).$
Then
![]() ${\mathcal E}(\frac {1}{\Delta }\mathbb {Z}\backslash \Lambda )$
is a Riesz basis for
${\mathcal E}(\frac {1}{\Delta }\mathbb {Z}\backslash \Lambda )$
is a Riesz basis for
![]() $L^2([0,\Delta ]\backslash S).$
$L^2([0,\Delta ]\backslash S).$
Proof of Theorem 1.2
Let
![]() $\beta $
and
$\beta $
and
![]() $b_k$
be real numbers as in Theorem 1.2. First, we introduce the interval
$b_k$
be real numbers as in Theorem 1.2. First, we introduce the interval
![]() $[0,\Delta ],$
where
$[0,\Delta ],$
where
![]() $\Delta =\lceil \frac {1+b_{m-1}}{\beta } \rceil \beta $
and
$\Delta =\lceil \frac {1+b_{m-1}}{\beta } \rceil \beta $
and
![]() $\lceil x \rceil $
is a ceiling function. The set J defined as (1.1) will be a subset of
$\lceil x \rceil $
is a ceiling function. The set J defined as (1.1) will be a subset of
![]() $[0,\Delta ].$
Let
$[0,\Delta ].$
Let
![]() $\Lambda =\{n+\delta ^*_n\}_{n\in \mathbb {Z}}=\{\lambda _n\}_{n\in \mathbb {Z}},$
where
$\Lambda =\{n+\delta ^*_n\}_{n\in \mathbb {Z}}=\{\lambda _n\}_{n\in \mathbb {Z}},$
where
 $$ \begin{align*} \begin{aligned} \lambda_n&=\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta} , & \text{if } \{\beta n\} < \frac12.\\ \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lambda_n&=\begin{cases} \frac{\lfloor \beta n \rfloor+1}{\beta}, & \text{if } \{\beta n\} \geq \frac12, \\ \frac{\lfloor \beta n \rfloor}{\beta} , & \text{if } \{\beta n\} < \frac12.\\ \end{cases} \end{aligned} \end{align*} $$
In view of the definition of
![]() $\beta $
, we have that
$\beta $
, we have that
![]() $\Lambda \subset \frac {1}{\Delta }\mathbb {Z}.$
By Theorem 1.1,
$\Lambda \subset \frac {1}{\Delta }\mathbb {Z}.$
By Theorem 1.1,
![]() ${\mathcal E}(\Lambda )$
is a Riesz basis for
${\mathcal E}(\Lambda )$
is a Riesz basis for
![]() $L^2(J).$
So, by Theorem 3.4,
$L^2(J).$
So, by Theorem 3.4,
![]() ${\mathcal E}(\frac {1}{\Delta }\mathbb {Z}\backslash \Lambda )$
is a Riesz basis for
${\mathcal E}(\frac {1}{\Delta }\mathbb {Z}\backslash \Lambda )$
is a Riesz basis for
![]() $L^2([0,\Delta ]\backslash J).$
$L^2([0,\Delta ]\backslash J).$
4 Extensions and generalizations
4.1 A stability theorem
Theorem 4.1 (Stability theorem for m-segments). Let
![]() $m\in \mathbb {N}\backslash \{1\}$
and
$m\in \mathbb {N}\backslash \{1\}$
and
![]() $b_j \in \mathbb {N}$
for all
$b_j \in \mathbb {N}$
for all
![]() $j=1,\ldots ,m-1$
and
$j=1,\ldots ,m-1$
and
![]() $L:=\sup _n |\delta _n|<\frac {1}{4}.$
Then the system
$L:=\sup _n |\delta _n|<\frac {1}{4}.$
Then the system
![]() $\{e^{2\pi i(n+\delta _n)x}\}$
is a Riesz basis for
$\{e^{2\pi i(n+\delta _n)x}\}$
is a Riesz basis for
![]() $L^2(J)$
if for all
$L^2(J)$
if for all
![]() $j=1,\ldots ,m-1$
and
$j=1,\ldots ,m-1$
and
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
where
 $$ \begin{align} \begin{aligned} A&=A(L)=\cos(\pi L) - \sin(\pi L),\\ B_{\gamma_j}&=B_{\gamma_j}(L)=2-\cos{(\pi \gamma_j L)}+\sin{(\pi \gamma_j L)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} A&=A(L)=\cos(\pi L) - \sin(\pi L),\\ B_{\gamma_j}&=B_{\gamma_j}(L)=2-\cos{(\pi \gamma_j L)}+\sin{(\pi \gamma_j L)}. \end{aligned} \end{align} $$
Proof By the
![]() $\frac {1}{4}$
-Kadec theorem, if
$\frac {1}{4}$
-Kadec theorem, if
![]() $L:=\sup _n |\delta _n|< \frac {1}{4},$
then
$L:=\sup _n |\delta _n|< \frac {1}{4},$
then
![]() $e^{2\pi i x (n+\delta _n)}$
is the Riesz basis for
$e^{2\pi i x (n+\delta _n)}$
is the Riesz basis for
![]() $L^2(I)$
with constants
$L^2(I)$
with constants
![]() $A=\cos {(\pi L)} - \sin {(\pi L)}$
and
$A=\cos {(\pi L)} - \sin {(\pi L)}$
and
![]() $B=2-\cos {(\pi L)} + \sin {(\pi L)}.$
Then, using Lemma 2.11, we can obtain a Riesz basis
$B=2-\cos {(\pi L)} + \sin {(\pi L)}.$
Then, using Lemma 2.11, we can obtain a Riesz basis
![]() $\{g_n\}_{n\in \mathbb {Z}}$
for
$\{g_n\}_{n\in \mathbb {Z}}$
for
![]() $L^2(J),$
where
$L^2(J),$
where
 $$ \begin{align*}g_n=\sum_{k=0}^{m} e^{2\pi i x \lambda_n}e^{2\pi i b_k \lambda_n}\chi_{J_k}.\end{align*} $$
$$ \begin{align*}g_n=\sum_{k=0}^{m} e^{2\pi i x \lambda_n}e^{2\pi i b_k \lambda_n}\chi_{J_k}.\end{align*} $$
Next, we are going to use Theorem 2.4 with the norm
We can estimate the right-hand side of the inequality using substitution and the Riesz sequence definition as
 $$ \begin{align*} \begin{aligned} ||\sum a_n g_n||_{L^{2,\infty}(J)}&\geq \frac{1}{\sqrt{m}}||\sum a_n g_n||_{L^2(J)}\\ &=\frac{1}{\sqrt{m}}||\sum a_n e^{i(n+\delta_n)x}||_{L^2(I)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} ||\sum a_n g_n||_{L^{2,\infty}(J)}&\geq \frac{1}{\sqrt{m}}||\sum a_n g_n||_{L^2(J)}\\ &=\frac{1}{\sqrt{m}}||\sum a_n e^{i(n+\delta_n)x}||_{L^2(I)}. \end{aligned} \end{align*} $$
By the elementary inequality
![]() $\sum \{|a_1|,...,|a_m|\}\geq \frac {1}{\sqrt (m)}\sqrt {\sum _n|a_n|^2}$
, we have
$\sum \{|a_1|,...,|a_m|\}\geq \frac {1}{\sqrt (m)}\sqrt {\sum _n|a_n|^2}$
, we have
For the left-hand side, we have
 $$ \begin{align*} \begin{aligned} ||\sum a_n \left(g_n- e^{2 \pi i(n+\delta_n)x}\right)||_{L^{2,\infty}(J)}&\leq \max_{j=1,...,m}||\sum a_n e^{2\pi i(n+\delta_n)x}\left(e^{-2\pi i(n+\delta_n)b_j}- 1\right)||_{L^{2,\infty}(J_j)}\\ &\leq \max_{j=1,...,m}\Bigg\{ B_{\gamma_j}\sqrt{\sum \left|a_n \left(e^{-2\pi i(n+\delta_n)b_j}- 1\right)\right|{}^2}\Bigg\}\\ &\leq 2 \max_{j=1,...,m} \{B_j \sup_n{|\sin{(\pi(n+\delta_n)b_j)}|}\}\\ &= 2 \max_{j=1,...,m} \{B_{\gamma_j} \sup_n{|\sin{(\pi\delta_nb_j)}|}\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} ||\sum a_n \left(g_n- e^{2 \pi i(n+\delta_n)x}\right)||_{L^{2,\infty}(J)}&\leq \max_{j=1,...,m}||\sum a_n e^{2\pi i(n+\delta_n)x}\left(e^{-2\pi i(n+\delta_n)b_j}- 1\right)||_{L^{2,\infty}(J_j)}\\ &\leq \max_{j=1,...,m}\Bigg\{ B_{\gamma_j}\sqrt{\sum \left|a_n \left(e^{-2\pi i(n+\delta_n)b_j}- 1\right)\right|{}^2}\Bigg\}\\ &\leq 2 \max_{j=1,...,m} \{B_j \sup_n{|\sin{(\pi(n+\delta_n)b_j)}|}\}\\ &= 2 \max_{j=1,...,m} \{B_{\gamma_j} \sup_n{|\sin{(\pi\delta_nb_j)}|}\}, \end{aligned} \end{align*} $$
where
![]() $B_{\gamma _j}= 2 - \cos {(\pi \gamma _j L)} + \sin {(\pi \gamma _j L)}$
for
$B_{\gamma _j}= 2 - \cos {(\pi \gamma _j L)} + \sin {(\pi \gamma _j L)}$
for
![]() $j=1,...,m-1.$
So, we need
$j=1,...,m-1.$
So, we need
or
Remark 4.2 If
![]() $m=1$
, we only have one interval, so Kadec’s theorem holds.
$m=1$
, we only have one interval, so Kadec’s theorem holds.
Remark 4.3 Observe that
![]() $A(L)$
defined as (4.2) is a concave down function of L on the interval
$A(L)$
defined as (4.2) is a concave down function of L on the interval
![]() $\left [0,\frac 14\right )$
and
$\left [0,\frac 14\right )$
and
![]() $B_{\gamma _j}(L)$
defined as (4.2) is a concave up function of L on the interval
$B_{\gamma _j}(L)$
defined as (4.2) is a concave up function of L on the interval
![]() $\left [0,\frac {1}{4\gamma _j}\right )$
for
$\left [0,\frac {1}{4\gamma _j}\right )$
for
![]() $j=1,...,m-1.$
Also, we can use the fact that
$j=1,...,m-1.$
Also, we can use the fact that
![]() $\sin (\pi \mbox {dist}(\delta _nb_j, \mathbb {Z})) \leq \pi \mbox {dist}(\delta _nb_j, \mathbb {Z}). $
So, the condition
$\sin (\pi \mbox {dist}(\delta _nb_j, \mathbb {Z})) \leq \pi \mbox {dist}(\delta _nb_j, \mathbb {Z}). $
So, the condition
 $$ \begin{align*}\max_{j=1,...,m-1} \{(1+4L\gamma_j)\,\mbox{dist}(\mathbb{Z}, \delta_nb_j)\} \leq \frac{ (1-4 L)}{2 \sqrt{m}\pi}, \end{align*} $$
$$ \begin{align*}\max_{j=1,...,m-1} \{(1+4L\gamma_j)\,\mbox{dist}(\mathbb{Z}, \delta_nb_j)\} \leq \frac{ (1-4 L)}{2 \sqrt{m}\pi}, \end{align*} $$
for
![]() $j=1,...,m-1,$
guarantees that (4.1) holds.
$j=1,...,m-1,$
guarantees that (4.1) holds.
4.2 d-dimensions
We use the arguments developed in previous sections to find bases on “split cubes.” Let
![]() $Q=[0,1)^d$
, and let
$Q=[0,1)^d$
, and let
![]() $0=a_{0,k}<a_{1,k}<\cdots <a_{m_k-1,k}<\cdots <1$
, where
$0=a_{0,k}<a_{1,k}<\cdots <a_{m_k-1,k}<\cdots <1$
, where
![]() $m_k\in \mathbb {N}\cup \{\infty \},$
for all
$m_k\in \mathbb {N}\cup \{\infty \},$
for all
![]() $k=1,...,d.$
Also, we let
$k=1,...,d.$
Also, we let
![]() $I_{j,k}=[a_{j,k}, a_{j+1,k})$
and
$I_{j,k}=[a_{j,k}, a_{j+1,k})$
and
so
Given that for all
![]() $k=1,...,d,$
we have
$k=1,...,d,$
we have
![]() $0=b_{0,k}<b_{1,k}<\cdots <b_{m_k-1,k}$
, and we let
$0=b_{0,k}<b_{1,k}<\cdots <b_{m_k-1,k}$
, and we let
![]() $\vec {\beta }_{\vec {j}}=(b_{j_1,1},b_{j_2,2},...,b_{j_d,d}).$
Now, we can define a “split cube” as
$\vec {\beta }_{\vec {j}}=(b_{j_1,1},b_{j_2,2},...,b_{j_d,d}).$
Now, we can define a “split cube” as
 $$ \begin{align} \tilde Q=\bigcup_{\vec{j}} \left(\tau_{\vec{\beta}_{\vec{j}}}+R_{\vec{j}}\right). \end{align} $$
$$ \begin{align} \tilde Q=\bigcup_{\vec{j}} \left(\tau_{\vec{\beta}_{\vec{j}}}+R_{\vec{j}}\right). \end{align} $$
Let
![]() $\beta _k>0$
be fixed for
$\beta _k>0$
be fixed for
![]() $k=1,...,d$
; for every
$k=1,...,d$
; for every
![]() $n_k\in \mathbb {Z}$
, we let
$n_k\in \mathbb {Z}$
, we let
 $$ \begin{align} \delta_{n_k}^*=\begin{cases} \frac{\lfloor \beta_k n_k \rfloor+1}{\beta_k}-n_k, & \text{if } \{\beta_k n_k\} \geq \frac12, \\ \frac{\lfloor \beta_k n_k \rfloor}{\beta_k}-n_k, & \text{if } \{\beta_k n_k\} < \frac12.\\ \end{cases} \end{align} $$
$$ \begin{align} \delta_{n_k}^*=\begin{cases} \frac{\lfloor \beta_k n_k \rfloor+1}{\beta_k}-n_k, & \text{if } \{\beta_k n_k\} \geq \frac12, \\ \frac{\lfloor \beta_k n_k \rfloor}{\beta_k}-n_k, & \text{if } \{\beta_k n_k\} < \frac12.\\ \end{cases} \end{align} $$
We let
![]() $\vec {\delta }_{n}^*=(\delta _{n_1}^*,...,\delta _{n_d}^*).$
Let
$\vec {\delta }_{n}^*=(\delta _{n_1}^*,...,\delta _{n_d}^*).$
Let
 $$ \begin{align} \begin{aligned} {\mathcal{B}}_k^* &=\{e^{2\pi i x_k(n_k+\delta_{n_k}^*)}\}_{n_k\in\mathbb{Z} },\\ {\mathcal{B}}^*&= \{e^{2\pi i x\cdot (n +\vec\delta_{n }^*) }\}_{n \in\mathbb{Z}^d} \quad \mbox{ with } x\in\mathbb{R}^d. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\mathcal{B}}_k^* &=\{e^{2\pi i x_k(n_k+\delta_{n_k}^*)}\}_{n_k\in\mathbb{Z} },\\ {\mathcal{B}}^*&= \{e^{2\pi i x\cdot (n +\vec\delta_{n }^*) }\}_{n \in\mathbb{Z}^d} \quad \mbox{ with } x\in\mathbb{R}^d. \end{aligned} \end{align} $$
Lemma 2.1 in [Reference Sun and Zhou23] can be generalized in the following way.
Lemma 4.4 Let each the set
![]() ${\mathcal U}_j=\{e^{2\pi i x \lambda _{j }(n)}\}_{n \in \mathbb {Z}}$
be a basis on a domain
${\mathcal U}_j=\{e^{2\pi i x \lambda _{j }(n)}\}_{n \in \mathbb {Z}}$
be a basis on a domain
![]() $D_j\subset \mathbb {R}$
, with constants
$D_j\subset \mathbb {R}$
, with constants
![]() $A_j$
and
$A_j$
and
![]() $B_j,$
then the set
$B_j,$
then the set
![]() $\{e^{2\pi i ( \lambda _1(n_1)x_1 +\cdots + \lambda _d(n_d) x_d }\}_{n_1, ..., n_d \in \mathbb {Z} } $
is a basis on
$\{e^{2\pi i ( \lambda _1(n_1)x_1 +\cdots + \lambda _d(n_d) x_d }\}_{n_1, ..., n_d \in \mathbb {Z} } $
is a basis on
![]() $L^2( D_1\times \cdots \times D_d), $
with the constants
$L^2( D_1\times \cdots \times D_d), $
with the constants
![]() $A=A_1\cdot ...\cdot A_d$
and
$A=A_1\cdot ...\cdot A_d$
and
![]() $B=B_1\cdot ...\cdot B_d.$
$B=B_1\cdot ...\cdot B_d.$
Proof We consider only the case
![]() $d=2.$
If
$d=2.$
If
![]() $d>2,$
the proof is similar. Let
$d>2,$
the proof is similar. Let
![]() ${\mathcal U}_j=\{e^{2\pi i x (\lambda _{j }(n)}\}_{n \in \mathbb {Z}}$
be a basis on a domain
${\mathcal U}_j=\{e^{2\pi i x (\lambda _{j }(n)}\}_{n \in \mathbb {Z}}$
be a basis on a domain
![]() $D_j\subset \mathbb {R}$
, with constants
$D_j\subset \mathbb {R}$
, with constants
![]() $A_j$
and
$A_j$
and
![]() $B_j$
,
$B_j$
,
![]() $j=1,2.$
Also, to simplify formulas, we use the following notations:
$j=1,2.$
Also, to simplify formulas, we use the following notations:
For any
![]() $f\in L^2(D_1\times D_2),$
we have
$f\in L^2(D_1\times D_2),$
we have
 $$ \begin{align*} \begin{aligned} \sum_{n_1, n_2\in \mathbb{Z}} |\langle f, \tilde v_{n_1,n_2}\rangle_{L^2(D_1\times D_2)} |^2 &= \sum_{n_2} \sum_{n_1} \left|\int_{D_1} \left(\int_{D_2} f(x_1,x_2)v_{2,n_2} dx_2\right) v_{1,n_1} dx_1\right|{}^2\\ &\leq B_1 \int_{D_1} \sum_{n_2} \left| \int_{D_2} f(x_1,x_2)v_{2,n_2} dx_2\right|{}^2 dx_1\\ &\leq B_1 B_2 \left\lVert f\right\rVert_{L^2(D_1\times D_2)}^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{n_1, n_2\in \mathbb{Z}} |\langle f, \tilde v_{n_1,n_2}\rangle_{L^2(D_1\times D_2)} |^2 &= \sum_{n_2} \sum_{n_1} \left|\int_{D_1} \left(\int_{D_2} f(x_1,x_2)v_{2,n_2} dx_2\right) v_{1,n_1} dx_1\right|{}^2\\ &\leq B_1 \int_{D_1} \sum_{n_2} \left| \int_{D_2} f(x_1,x_2)v_{2,n_2} dx_2\right|{}^2 dx_1\\ &\leq B_1 B_2 \left\lVert f\right\rVert_{L^2(D_1\times D_2)}^2. \end{aligned} \end{align*} $$
A similar argument shows that
Thus,
![]() $\{e^{2\pi i (\lambda _1(n_1)x_1 + \lambda _2(n_2)x_2 }\}_{n_1, n_2 \in \mathbb {Z} } $
is a frame for
$\{e^{2\pi i (\lambda _1(n_1)x_1 + \lambda _2(n_2)x_2 }\}_{n_1, n_2 \in \mathbb {Z} } $
is a frame for
![]() $L^2(D_1\times D_2).$
Next, for any finite sequence of complex numbers
$L^2(D_1\times D_2).$
Next, for any finite sequence of complex numbers
![]() $c_{n_1,n_2 }$
, we have
$c_{n_1,n_2 }$
, we have
 $$ \begin{align*} \begin{aligned} \Big\Vert \sum_{n_1}\sum_{n_2} c_{n_1,n_2 } \tilde v_{n_1,n_2} \Big\Vert^2 &=\int_{D_2} \int_{D_1} \left|\sum_{n_1} \left(\sum_{n_2} c_{n_1,n_2 } v_{2,n_2} \right) v_{1,n_1} \right|{}^2 dx_1dx_2 \\ &\leq B_1 \sum_{n_1} \int_{D_2} \left| \sum_{n_2} c_{n_1,n_2 } v_{2,n_2} \right|{}^2 dx_2\\ &\leq B_1 B_2 \sum_{n_1} \sum_{n_2} \left| c_{n_1,n_2 } \right|{}^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Big\Vert \sum_{n_1}\sum_{n_2} c_{n_1,n_2 } \tilde v_{n_1,n_2} \Big\Vert^2 &=\int_{D_2} \int_{D_1} \left|\sum_{n_1} \left(\sum_{n_2} c_{n_1,n_2 } v_{2,n_2} \right) v_{1,n_1} \right|{}^2 dx_1dx_2 \\ &\leq B_1 \sum_{n_1} \int_{D_2} \left| \sum_{n_2} c_{n_1,n_2 } v_{2,n_2} \right|{}^2 dx_2\\ &\leq B_1 B_2 \sum_{n_1} \sum_{n_2} \left| c_{n_1,n_2 } \right|{}^2. \end{aligned} \end{align*} $$
A similar argument shows that
 $$ \begin{align*} \begin{aligned} \Big\Vert \sum_{n_1}\sum_{n_2} c_{n_1,n_2 } \tilde v_{n_1,n_2} \Big\Vert^2 &\geq A_1 A_2 \sum_{n_1} \sum_{n_2} \left| c_{n_1,n_2 } \right|{}^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Big\Vert \sum_{n_1}\sum_{n_2} c_{n_1,n_2 } \tilde v_{n_1,n_2} \Big\Vert^2 &\geq A_1 A_2 \sum_{n_1} \sum_{n_2} \left| c_{n_1,n_2 } \right|{}^2. \end{aligned} \end{align*} $$
Therefore,
![]() $\{e^{2\pi i (\lambda _1(n_1)x_1 + \lambda _2(n_2)x_2 }\}_{n_1, n_2 \in \mathbb {Z} } $
is a basis for
$\{e^{2\pi i (\lambda _1(n_1)x_1 + \lambda _2(n_2)x_2 }\}_{n_1, n_2 \in \mathbb {Z} } $
is a basis for
![]() $L^2(D_1\times D_2).$
Moreover,
$L^2(D_1\times D_2).$
Moreover,
![]() $A=A_1\cdot A_2$
and
$A=A_1\cdot A_2$
and
![]() $B=B_1\cdot B_2$
are the Riesz constants.
$B=B_1\cdot B_2$
are the Riesz constants.
Now, we can use Lemma 4.4 to generalize some results from Section 3 in d-dimensions.
Lemma 4.5 For all
![]() $k=1,...,d,$
let
$k=1,...,d,$
let
![]() $\beta _k\geq 1.$
Then
$\beta _k\geq 1.$
Then
![]() ${\mathcal {B}}^*$
is an exponential basis for
${\mathcal {B}}^*$
is an exponential basis for
![]() $L^2([0,1]^d),$
where
$L^2([0,1]^d),$
where
![]() ${\mathcal {B}}^*$
is defined as in (4.5).
${\mathcal {B}}^*$
is defined as in (4.5).
Proof From Lemma 3.1, we have that
![]() ${\mathcal {B}}^*_k,$
defined as in (4.5), is a basis for
${\mathcal {B}}^*_k,$
defined as in (4.5), is a basis for
![]() $L^2([0,1]).$
Therefore, by Lemma 4.5,
$L^2([0,1]).$
Therefore, by Lemma 4.5,
![]() ${\mathcal {B}}^*$
is an exponential basis for
${\mathcal {B}}^*$
is an exponential basis for
![]() $L^2([0,1]^d).$
$L^2([0,1]^d).$
Theorem 4.6 Let
![]() $\vec {m}=(m_1,...,m_d),$
when
$\vec {m}=(m_1,...,m_d),$
when
![]() $m_k\in \mathbb {N}\cup \{\infty \}$
. For all
$m_k\in \mathbb {N}\cup \{\infty \}$
. For all
![]() $k=1,...,d,$
let
$k=1,...,d,$
let
![]() $\beta _k\geq 1.$
If for all
$\beta _k\geq 1.$
If for all
![]() $k=1,...,d \ \frac {b_{j,k}}{\beta _k}\in \mathbb {Z} $
for all j, then the set
$k=1,...,d \ \frac {b_{j,k}}{\beta _k}\in \mathbb {Z} $
for all j, then the set
![]() ${\mathcal {B}}^*$
defined in (4.5) is an exponential basis for
${\mathcal {B}}^*$
defined in (4.5) is an exponential basis for
![]() $L^2(\tilde Q),$
where
$L^2(\tilde Q),$
where
![]() ${\mathcal {B}}^*$
is defined as in (4.5). Moreover,
${\mathcal {B}}^*$
is defined as in (4.5). Moreover,
![]() ${\mathcal {B}}^*$
has the same frame constants for
${\mathcal {B}}^*$
has the same frame constants for
![]() $L^2(\tilde Q)$
and
$L^2(\tilde Q)$
and
![]() $L^2(Q).$
$L^2(Q).$
5 Remarks and open problems
Theorem 1.1 provides explicit exponential bases for split intervals under conditions on
![]() $b_k.$
In Remark 3.3, we have observed that we can obtain the frame constants for the basis when
$b_k.$
In Remark 3.3, we have observed that we can obtain the frame constants for the basis when
![]() $b\geq 2.$
The problem of finding explicit exponential bases for general split intervals, and explicit frame constants for these bases, is still waiting for a solution. The same situation occurs with exponential bases on split cubes in
$b\geq 2.$
The problem of finding explicit exponential bases for general split intervals, and explicit frame constants for these bases, is still waiting for a solution. The same situation occurs with exponential bases on split cubes in
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
We have provided explicit exponential bases on certain infinite unions of intervals of total finite measure. We would like to generalize our results and prove the existence of exponential bases on arbitrary infinite unions of intervals or rectangles.
Our Theorem 4.1 reduces to Kadec’s theorem when the interval is not split, but in the other cases, we obtain stability bounds that depend on the gaps between the intervals. We believe that this result can be improved, and we hope to do so in another paper.
Acknowledgment
Foremost, we would like to express our sincere gratitude to our mentor Professor Laura De Carli for her continuous support of our research. We acknowledge the collaboration of Mark Leal and Izzy Morell in the initial stage of this project and their participation in the technical report (available at go.fiu.edu/amrpu).