The f-Chromatic Index of a Graph Whose f-Core Has Maximum Degree 2

Abstract.

Let $G$ be a graph. The minimum number of colors needed to color the edges of $G$ is called the chromatic index of $G$ and is denoted by 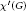$X'\left( G \right)$. It is well known that 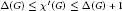$\Delta \left( G \right)\,\le \,\mathcal{X}'\left( G \right)\,\le \Delta \left( G \right)\,+\,1$, for any graph $G$, where 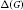$\Delta \left( G \right)$ denotes the maximum degree of $G$. A graph $G$ is said to be class 1 if 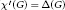${\mathcal{X}}'\left( G \right)\,=\,\Delta \left( G \right)$ and class 2 if 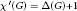${\mathcal{X}}'\left( G \right)\,=\,\Delta \left( G \right)\,+\,1$. Also, 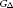${{G}_{\Delta }}$ is the induced subgraph on all vertices of degree 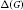$\Delta \left( G \right)$. Let 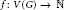$f:\,V\left( G \right)\,\to \mathbb{N}$ be a function. An $f$ -coloring of a graph $G$ is a coloring of the edges of 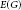$E\left( G \right)$ such that each color appears at each vertex 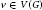$v\,\in \,V\left( G \right)$ at most 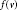$f\left( v \right)$ times. The minimum number of colors needed to $f$ -color $G$ is called the $f$ -chromatic index of $G$ and is denoted by 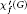${{{\mathcal{X}}'}_{f}}\left( G \right)$. It was shown that for every graph 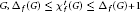$G,\,{{\Delta }_{f}}\,\left( G \right)\,\le \,{{\mathcal{X}}^{\prime }}_{f}\left( G \right)\,\le \,{{\Delta }_{f}}\,\left( G \right)\,+\,1$, where 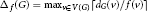${{\Delta }_{f}}\left( G \right)\,=\,{{\max }_{v\in \left( G \right)}}\,\left\lceil {{{d}_{G}}\left( v \right)}/{f\left( v \right)}\; \right\rceil $. 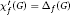A graph $G$ is said to be $f$ -class 1 if ${{\mathcal{X}}^{\prime }}_{f}\left( G \right)\,=\,{{\Delta }_{f}}\left( G \right)$, and $f$ -class 2, otherwise. Also, 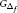${{G}_{{{\Delta }_{f}}}}$ is the induced subgraph of $G$ on 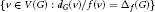$\left\{ v\,\in \,V\left( G \right)\,:\,{{{d}_{G}}\left( V \right)}/{f\left( v \right)}\;\,=\,{{\Delta }_{f}}\left( G \right) \right\}$. 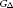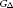Hilton and Zhao showed that if ${{G}_{\Delta }}$ has maximum degree two and $G$ is class 2, then $G$ is critical, ${{G}_{\Delta }}$ is a disjoint union of cycles and 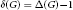$\delta \left( G \right)\,=\,\Delta \left( G \right)-1$, where 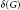$\delta \left( G \right)$ denotes the minimum degree of $G$, respectively. In this paper, we generalize this theorem to $f$ -coloring of graphs. Also, we determine the $f$ -chromatic index of a connected graph $G$ with 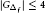$\left| {{G}_{{{\Delta }_{f}}}} \right|\,\le \,4$.