Published online by Cambridge University Press: 20 November 2018
In this paper, we explore a generalization of the notion of integrality. In particular, we study a near-integrality condition that is intermediate between the concepts of integral and almost integral. This property (referred to as the 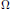 $\Omega $-almost integral property) is a representative independent specialization of the standard notion of almost integrality. Some of the properties of this generalization are explored in this paper, and these properties are compared with the notion of pseudo-integrality introduced by Anderson, Houston, and Zafrullah. Additionally, it is shown that the
$\Omega $-almost integral property) is a representative independent specialization of the standard notion of almost integrality. Some of the properties of this generalization are explored in this paper, and these properties are compared with the notion of pseudo-integrality introduced by Anderson, Houston, and Zafrullah. Additionally, it is shown that the 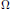 $\Omega $-almost integral property serves to characterize the survival/lying over pairs of Dobbs and Coykendall.
$\Omega $-almost integral property serves to characterize the survival/lying over pairs of Dobbs and Coykendall.