Published online by Cambridge University Press: 20 November 2018
The generating degree 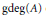 $\text{g}\deg \left( A \right)$ of a topological commutative ring
$\text{g}\deg \left( A \right)$ of a topological commutative ring 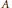 $A$ with char
$A$ with char 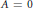 $A\,=\,0$ is the cardinality of the smallest subset
$A\,=\,0$ is the cardinality of the smallest subset 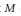 $M$ of
$M$ of 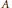 $A$ for which the subring
$A$ for which the subring 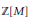 $\mathbb{Z}\left[ M \right]$ is dense in
$\mathbb{Z}\left[ M \right]$ is dense in 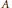 $A$. For a prime number
$A$. For a prime number 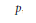 $p$,
$p$, 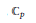 ${{\mathbb{C}}_{p}}$ denotes the topological completion of an algebraic closure of the field
${{\mathbb{C}}_{p}}$ denotes the topological completion of an algebraic closure of the field 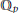 ${{\mathbb{Q}}_{p}}$ of
${{\mathbb{Q}}_{p}}$ of 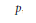 $p$-adic numbers. We prove that
$p$-adic numbers. We prove that 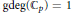 $\text{g}\deg \left( {{\mathbb{C}}_{p}} \right)\,=\,1$, i.e., there exists
$\text{g}\deg \left( {{\mathbb{C}}_{p}} \right)\,=\,1$, i.e., there exists  $t$ in
$t$ in 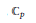 ${{\mathbb{C}}_{p}}$ such that
${{\mathbb{C}}_{p}}$ such that 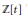 $\mathbb{Z}\left[ t \right]$ is dense in
$\mathbb{Z}\left[ t \right]$ is dense in 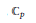 ${{\mathbb{C}}_{p}}$. We also compute
${{\mathbb{C}}_{p}}$. We also compute 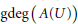 $\text{gdeg}\left( A\left( U \right) \right)$ where
$\text{gdeg}\left( A\left( U \right) \right)$ where 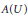 $A\left( U \right)$ is the ring of rigid analytic functions defined on a ball
$A\left( U \right)$ is the ring of rigid analytic functions defined on a ball 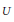 $U$ in
$U$ in 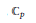 ${{\mathbb{C}}_{p}}$. If
${{\mathbb{C}}_{p}}$. If 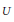 $U$ is a closed ball then
$U$ is a closed ball then 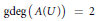 $\text{gdeg}\left( A\left( U \right) \right)\,=\,2$ while if
$\text{gdeg}\left( A\left( U \right) \right)\,=\,2$ while if 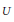 $U$ is an open ball then
$U$ is an open ball then 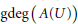 $\text{gdeg}\left( A\left( U \right) \right)$ is infinite. We show more generally that
$\text{gdeg}\left( A\left( U \right) \right)$ is infinite. We show more generally that 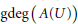 $\text{gdeg}\left( A\left( U \right) \right)$ is finite for any affinoid
$\text{gdeg}\left( A\left( U \right) \right)$ is finite for any affinoid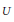 $U$ in
$U$ in 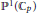 ${{\mathbb{P}}^{1}}\left( {{\mathbb{C}}_{p}} \right)$ and
${{\mathbb{P}}^{1}}\left( {{\mathbb{C}}_{p}} \right)$ and 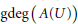 $\text{gdeg}\left( A\left( U \right) \right)$ is infinite for any wide open subset
$\text{gdeg}\left( A\left( U \right) \right)$ is infinite for any wide open subset 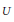 $U$ of
$U$ of 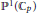 ${{\mathbb{P}}^{1}}\left( {{\mathbb{C}}_{p}} \right)$.
${{\mathbb{P}}^{1}}\left( {{\mathbb{C}}_{p}} \right)$.